Resistencia Equivalente

La manera en que se calcula la resistencia equivalente dependerá si está trabajando con un circuito en serie, paralelo o mixto.

Calcular la resistencia equivalente nos ayuda a obtener el valor de un resistor que puede reemplazar cualquier número de resistores conectados en un circuito ya sea que estén conectados en serie o en paralelo.

Te puede interesar: CALCULADORA DE RESISTENCIA EQUIVALENTE EN SERIE Y PARALELO

Resistencia equivalente en serie

En un circuito en serie la resistencia equivalente se obtiene realizando la suma algebraica de todas las resistencias que se encuentren dentro del circuito. Puede sonar como un término complejo, pero en realidad no lo es, y es de suma importancia para poder realizar cálculos y revisiones cuando se intentan obtener parámetros del circuito.

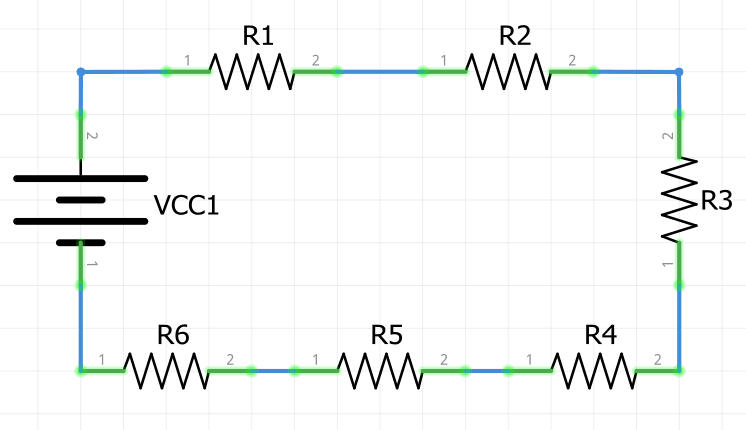
Después de encontrar la resistencia equivalente del circuito en serie, éste puede reducirse de la siguiente manera:

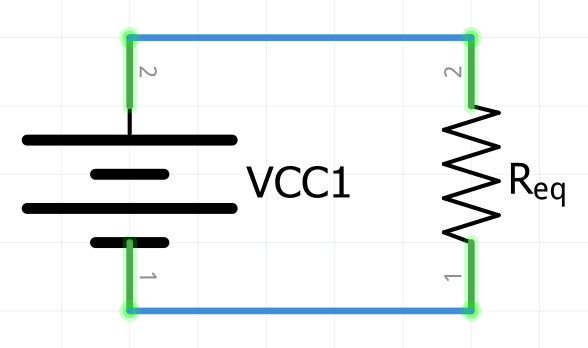
Fórmula para circuito en serie

Aún cuando se presenta un circuito con más de un componente, es posible calcular la resistencia efectiva total de todo el circuito o de una parte del circuito.

La resistencia equivalente del circuito conectado en Serie se encuentra simplemente sumando los valores de las resistencias individuales.

R_{eq}=R_1+R_2+R_3+...R_n

Ejercicios resueltos de resistencia equivalente circuito en serie

1.- Encontrar la resistencia equivalente del siguiente circuito:

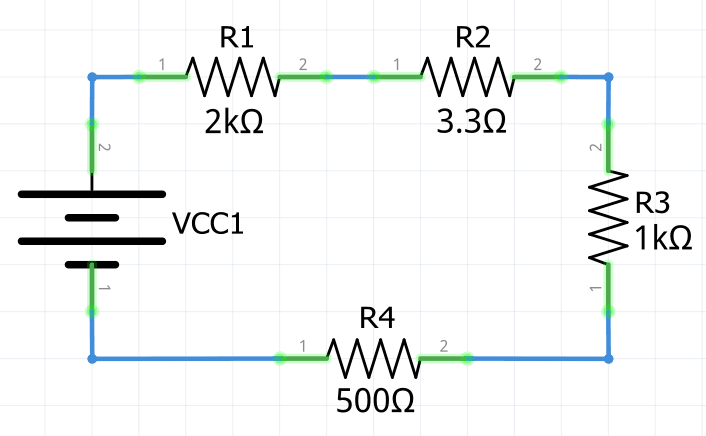
Se aplica la fórmula de Req en circuitos en serie utilizando los valores de los resistores que nos dan en la figura anterior.

La sustitución paso a paso de la fórmula y el resultado se muestran a continuación:

R_{eq}=R_1+R_2+R_3+R_4

R_{eq}=2000\Omega+3300\Omega+1000\Omega+500\Omega

R_{eq}=6800\Omega=\large\bold{6.8k\Omega}

Por lo tanto el circuito puede re dibujarse de la siguiente manera:

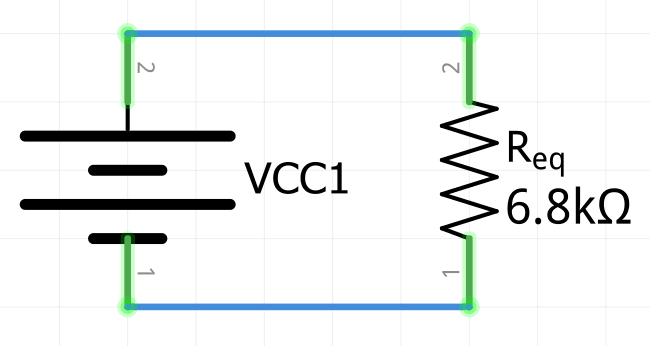
La resistencia equivalente es siempre mayor que cualquiera de las resistencias individuales en un circuito en serie.

Resistencia equivalente en paralelo

Un grupo de resistencias en paralelo puede ser reemplazado por una sola resistencia equivalente, que simplifica los cálculos cuando se intenta obtener parámetros de la red.

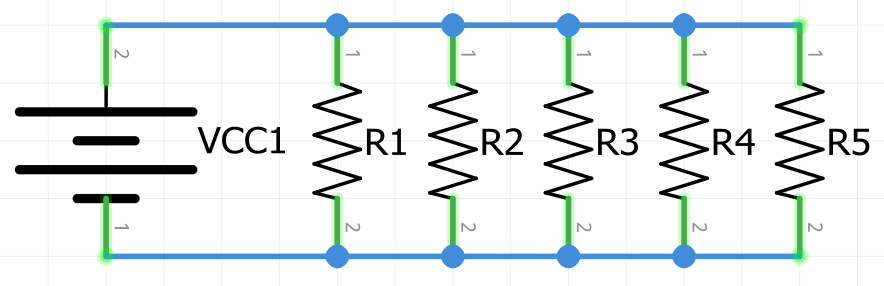
Después de encontrar la resistencia equivalente del circuito en paralelo, éste puede reducirse de la siguiente manera:

Fórmula para circuito en paralelo

Un circuito paralelo tiene propiedades que permiten calcular las resistencias individuales y la resistencia equivalente con una sola fórmula. La caída de voltaje es la misma en cada resistencia en paralelo.

En un circuito en Paralelo, el inverso multiplicativo de la Resistencia Equivalente se obtiene realizando la suma de los inversos multiplicativos de cada uno de los resistores.

\frac1{R_{eq}}=\frac1R_1+\frac1R_2+\frac1R_3+...\frac1R_n

Entonces despejando la expresión anterior, la resistencia equivalente también se obtiene con la siguiente fórmula:

R_{eq}=\frac1{\frac1R_1+\frac1R_2+\frac1R_3+...\frac1R_n}

Resistencia equivalente de dos o más Resistencias Iguales en Paralelo

Si el valor en ohms de dos o más resistencias en paralelo son iguales, se puede dividir dicho valor entre el número de resistencias iguales, y de esta manera obtener la resistencia equivalente:

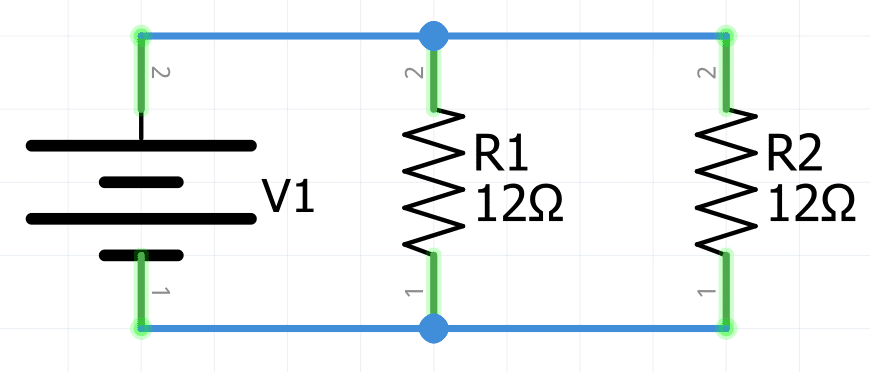
R_{eq}=12\Omega||12\Omega=\frac{12\Omega}{2}=\large\bold{6\Omega}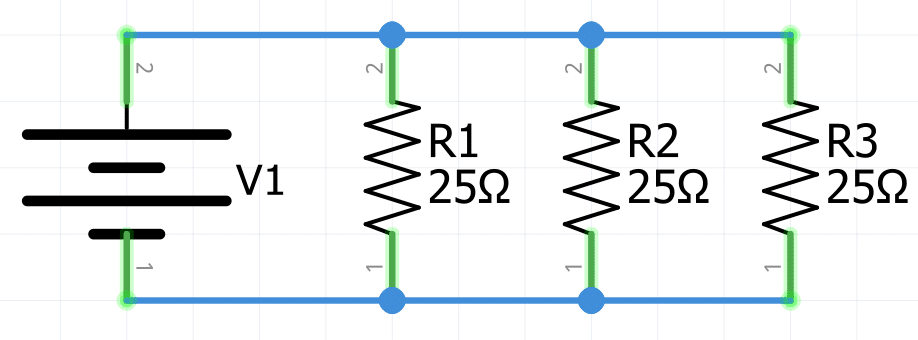

R_{eq}=25\Omega||25\Omega||25\Omega=\frac{25\Omega}{3}=\large\bold{8.3333\Omega}

Ejercicios resueltos de resistencia equivalente circuito paralelo

1.- Encontrar la resistencia equivalente del siguiente circuito:

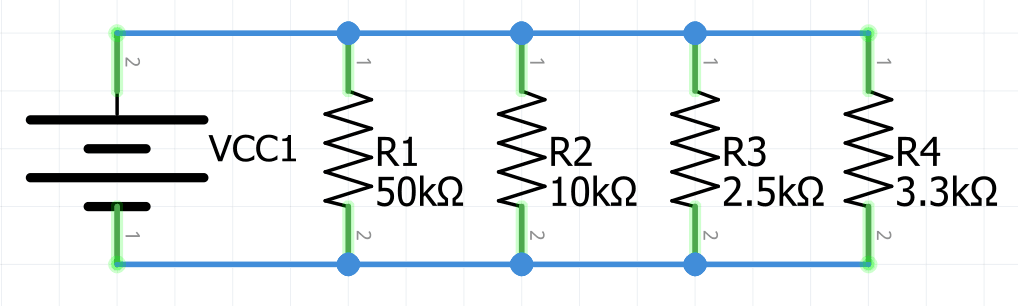
Primero se aplica la fórmula de Req para circuitos en paralelo utilizando los valores de los resistores de la figura anterior.

Luego, se realizan las operaciones correspondientes para obtener el resultado final de resistencia.

La sustitución paso a paso de la fórmula y el resultado se muestran a continuación:

R_{eq}=\frac1{\frac1{R_1}+\frac1{R_2}+\frac1{R_3}+\frac1{R_4}}

R_{eq}=\frac1{\frac1{50000\Omega}+\frac1{10000\Omega}+\frac1{2500\Omega}+\frac1{3300\Omega}}

R_{eq}=1215.022\Omega=\large\bold{1.215k\Omega}

Por lo tanto el circuito puede re dibujarse de la siguiente manera:

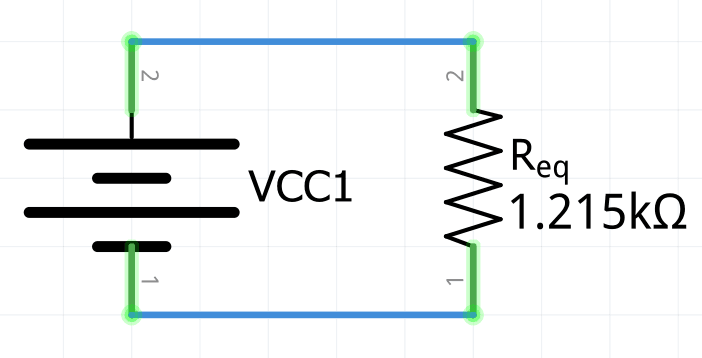
La resistencia equivalente es siempre menor que cualquiera de las resistencias individuales en un circuito en paralelo.

Resistencia equivalente en circuitos mixtos

Un circuito mixto es una combinación de varios elementos conectados tanto en paralelo como en serie, estos pueden colocarse de la manera que sea siempre y cuando se utilicen los dos diferentes sistemas de elementos, tanto paralelo como en serie.

Para calcular la Req de un circuito mixto debe ser capaz de reconocer los tipos de conexión de dicho circuito. Lo más recomendable es siempre iniciar la reducción desde el lado opuesto de la fuente de alimentación.

Ejercicios resueltos de resistencia equivalente para circuitos mixtos

1.- Encontrar la resistencia equivalente del siguiente circuito mixto:

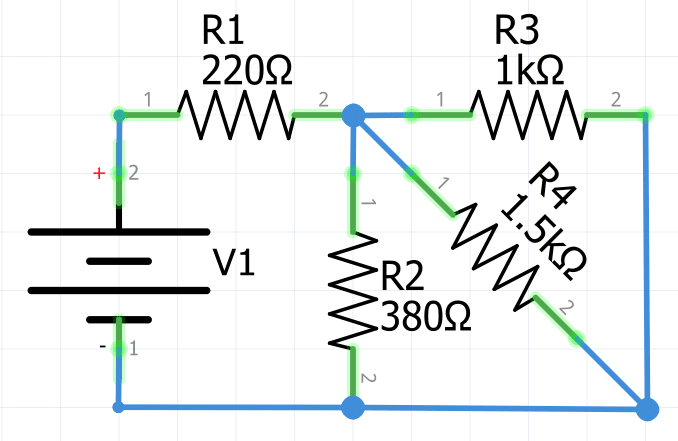
La reducción comienza del lado derecho del circuito, ya que R2, R3 y R4 se encuentran conectadas en paralelo. Si se aplica la fórmula de Req en paralelo a estas tres resistencias ( R2, R3 y R4 ) y se le nombra a esta nueva Resistencia como R5, se obtiene lo siguiente:

R_{5}=\frac1{\frac1{R_2}+\frac1{R_3}+\frac1{R_4}}

R_{5}=\frac1{\frac1{380\Omega}+\frac1{1000\Omega}+\frac1{1500\Omega}}

R_{5}=232.65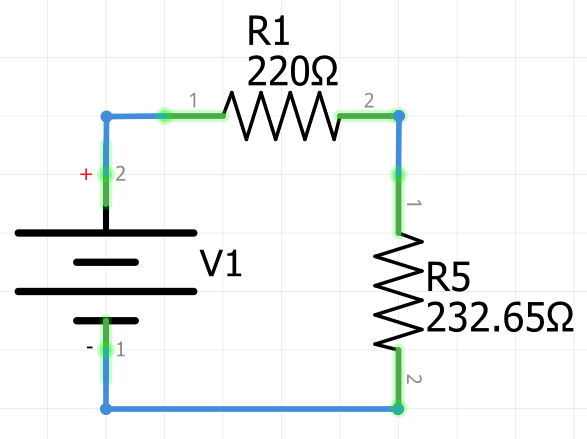

Una vez simplificada la resistencia R5, se tiene un circuito en serie con dos resistencias.

Ahora toca sacar la resistencia equivalente usando la fórmula para conexiones en serie:

R_{eq}=R_1+R_5

R_{eq}=220\Omega+232.65\Omega

R_{eq}=\large\bold{452.65\Omega}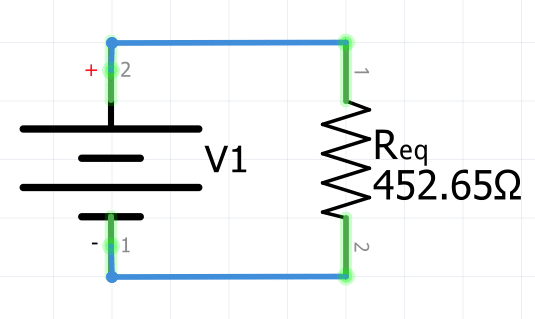

Entonces, para obtener la resistencia equivalente del circuito mixto se realizó la siguiente operación:

R_{eq}=R_1+(R_2||R_3||R_4)

Resumen