El teorema de Kennelly establece que cualquier red de tres terminales puede ser reemplazada por una impedancia delta o estrella equivalente sin perturbar la red externa. En otras palabras, este teorema permite determinar la carga en un circuito eléctrico en forma de estrella, a una dada en triángulo y viceversa.
El teorema de Kennelly también puede ser llamado transformación estrella-delta (Y-Δ) o transformación te-pi (T-Π).
Fórmulas
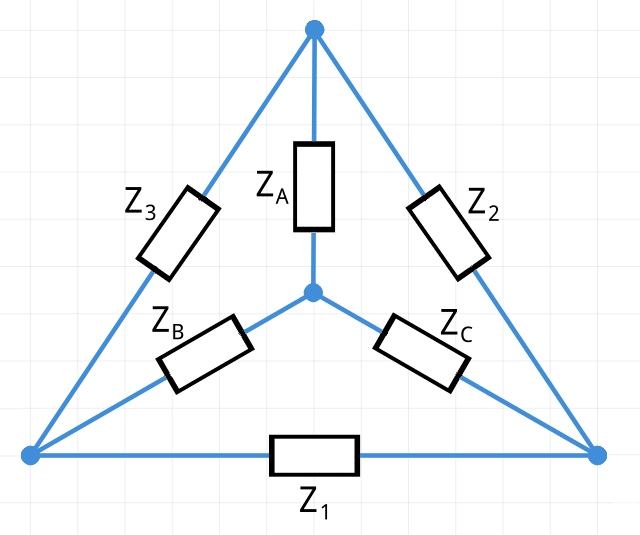
Según el teorema de Kennelly, los dos circuitos opuestos, el triángulo (o circuito en Π) y la estrella (o circuito en T) son circuitos equivalentes.
Transformación de delta a estrella (Δ-Y)
Las fórmulas que relacionan el reemplazo de una red delta (o triángulo) por una red equivalente estrella son las siguientes:
Z_{A}=\frac{Z_{2}Z_{3}}{Z_{1}+Z_{2}+Z_{3}}Z_{B}=\frac{Z_{1}Z_{3}}{Z_{1}+Z_{2}+Z_{3}}Z_{C}=\frac{Z_{1}Z_{2}}{Z_{1}+Z_{2}+Z_{3}}Transformación de estrella a delta (Y-Δ)
Las fórmulas que relacionan el reemplazo de una red estrella por una red equivalente delta (o triángulo) son las siguientes:

Z_{1}=\frac{Z_{A}Z_{B}+Z_{A}Z_{C}+Z_{B}Z_{C}}{Z_{A}}Z_{2}=\frac{Z_{A}Z_{B}+Z_{A}Z_{C}+Z_{B}Z_{C}}{Z_{B}}Z_{3}=\frac{Z_{A}Z_{B}+Z_{A}Z_{C}+Z_{B}Z_{C}}{Z_{C}}Ejercicios resueltos
En el análisis de circuitos suelen surgir situaciones en las que los resistores o las impedancias no están en paralelo ni en serie. En algunas ocasiones, esta situación puede resolverse al probar con la transformación estrella-delta y viceversa.
Transformación triángulo a estrella (AC)
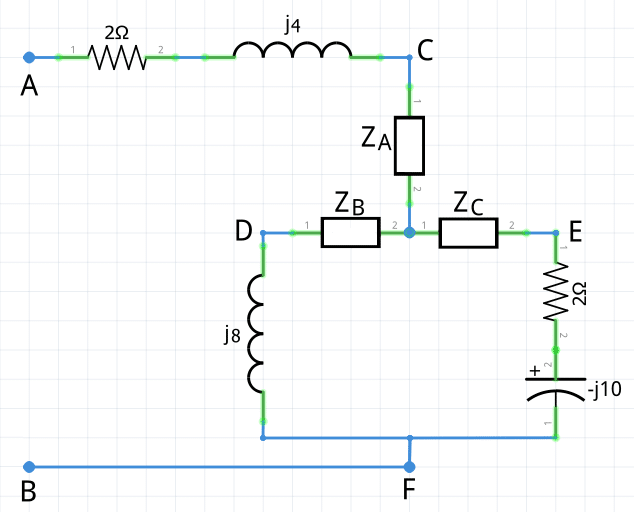
Encuentra la impedancia equivalente del siguiente circuito con inductores, resistores y condensadores, apoyándote del teorema de Kennelly (transformación delta-estrella).
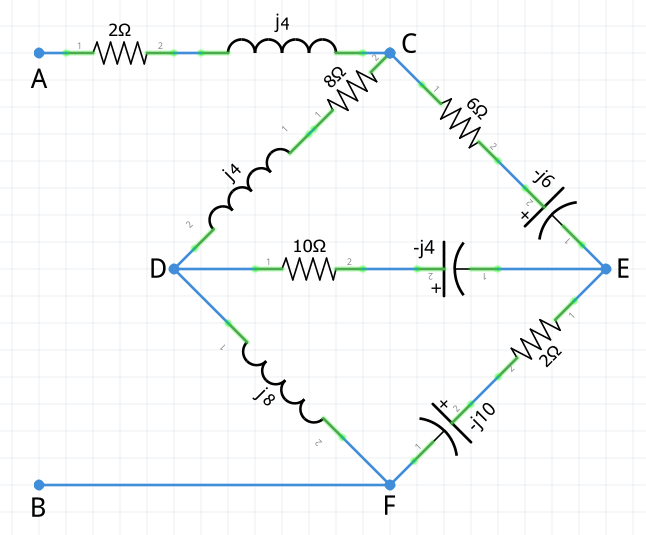
Se puede aplicar el teorema de Kennelly tanto al triángulo C-D-E como al triángulo D-E-F para hacer la reducción triángulo-estrella y poder obtener la impedancia equivalente.
Sea cual sea el triángulo que escojas para la reducción, el resultado final de la impedancia equivalente debe ser el mismo. En este ejercicio se le aplicará el teorema de Kennelly al triángulo C-D-E:
Z_{A}=\frac{(6-6j)(8+4j)}{(10-4j)+(6-6j)+(8+4j)}Z_{B}=\frac{(10-4j)(8+4j)}{(10-4j)+(6-6j)+(8+4j)}Z_{C}=\frac{(10-4j)(6+6j)}{(10-4j)+(6-6j)+(8+4j)}Realizando las operaciones correspondientes para cada inductancia se obtienen los siguientes resultados para Za, Zb y Zc:
Z_{A}=\frac{52}{17}-\frac{4j}{17}=(3.067\angle-4.398°)\OmegaZ_{B}=\frac{188}{51}-\frac{64j}{51}=(3.894\angle18.799°)\OmegaZ_{C}=\frac{50}{17}-\frac{38j}{17}=(3.694\angle37.234°)\OmegaPor lo tanto, nuestro circuito queda de la siguiente forma:
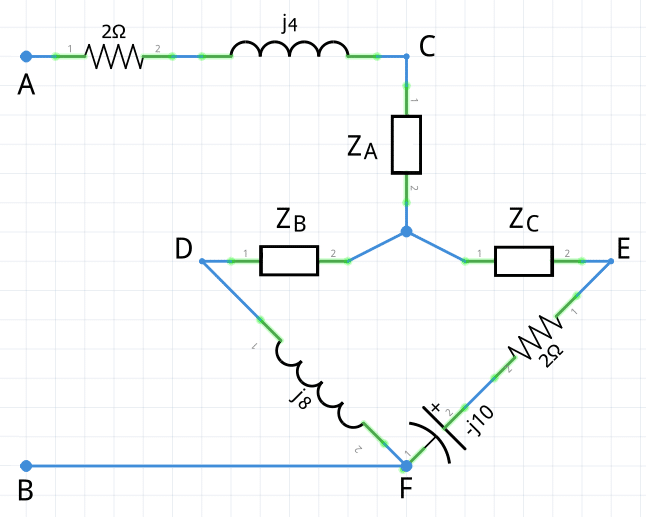
Una vez que se redibujan y organizan los componentes, se puede observar que la simplificación para la inductancia equivalente ahora está más clara. Se puede apreciar que con un par de reducciones de impedancias en paralelo y luego en serie, se llega fácilmente a la inductancia equivalente.
Z_{eq}=\bold{13.9882 + 8.08235 i=(16.16\angle30°)\Omega}Transformación estrella a triángulo (AC)
Aplique el teorema de Kennelly para cambiar el siguiente circuito en corriente alterna (con bobinas, resistencias y capacitores) a su forma equivalente delta.
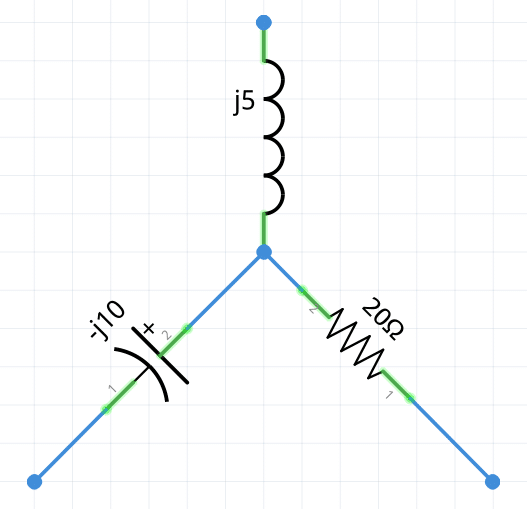
Primero se etiqueta cada componente de tal forma que sea más fácil sustituir cada valor en la fórmula del Teorema de Kennelly. Nombraremos a cada componente de la siguiente manera: Za=inductor/bobina, Zb=condensador/capacitor y Zc=resistor/resistencia.
Ahora si, aplicando las fórmulas para obtener el equivalente delta obtendremos los siguientes resultados:
Z_{1}=\frac{(5j)(-10j)+(5j)(20\Omega)+(-10j)(20\Omega)}{5j}Z_{2}=\frac{(5j)(-10j)+(5j)(20\Omega)+(-10j)(20\Omega)}{-10j}Z_{3}=\frac{(5j)(-10j)+(5j)(20\Omega)+(-10j)(20\Omega)}{20\Omega}Resolviendo cada una de las ecuaciones correspondientes a Z1, Z2 y Z3 se obtienen los resultados que finalmente se aplicarán al circuito equivalente delta.
Z_{1}=\bold{-20-10j=(22.36\angle-153.43°)\Omega}Z_{2}=\bold{10+5j=(11.18\angle26.56°)\Omega}Z_{3}=\bold{2.5-5j=(5.6\angle-63.43°)\Omega}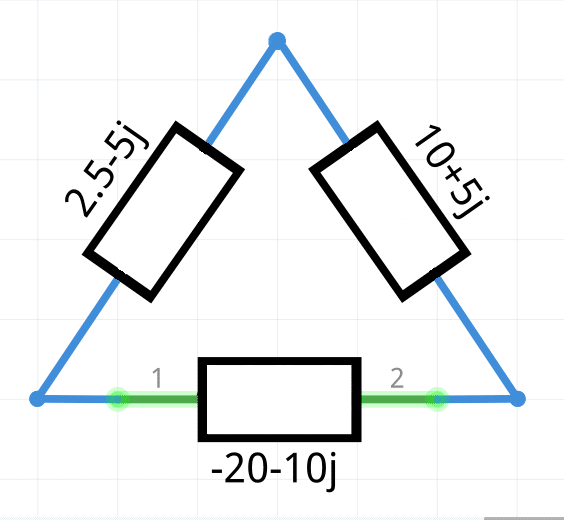
Submit your review | |







Una respuesta
cuál es el simulador donde puedo armar ese circuito?