
Existen dos formas básicas de conectar componentes eléctricos en un circuito: se pueden conectar mediante conexiones en serie o en paralelo.
Una tercer forma de circuito implica el uso dual de conexiones en serie y en paralelo; dichos circuitos se denominan circuito mixto o circuito combinado.
Definición
Un circuito mixto es una combinación de varios elementos conectados tanto en serie como en paralelo. Sus propiedades y características son una combinación de ambos tipos de conexión.
Los dos tipos de conexión presentes en los circuitos mixtos son la conexión en serie y en paralelo.
¿Cómo funciona?
En general, los circuitos mixtos tienen una fuente de alimentación conectada en serie con un interruptor que energiza todo el sistema por igual.
Después de este alimentador, generalmente hay varios circuitos secundarios cuya configuración varía de acuerdo con la estructuración de los receptores: circuitos en serie y paralelo sin un patrón específico.
Toma el siguiente circuito como ejemplo para saber cómo funciona un circuito mixto:
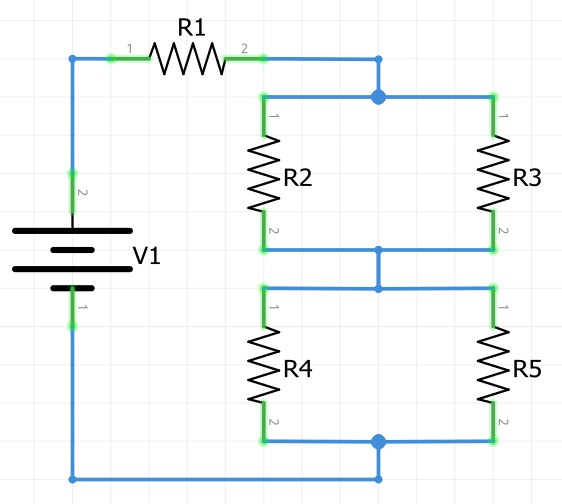
En este circuito la corriente sale de la parte inferior de la batería y se divide para viajar a través de R4 y R5, vuelve a unirse, luego se divide nuevamente para viajar a través de R2 y R3, vuelve a unirse para viajar a través de R1 y finalmente vuelve a la parte superior de la batería.
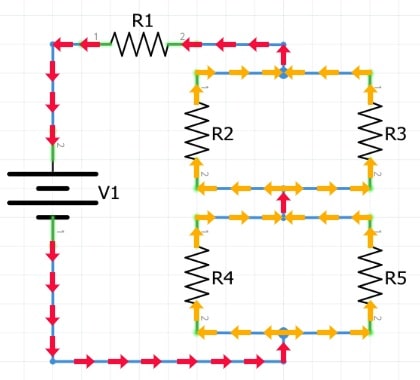
Entonces, existe más de una ruta para que la corriente viaje (circuito en paralelo), pero hay más de dos conjuntos de puntos eléctricamente comunes en el circuito (circuito en serie).
Para las conexiones en serie, todos los circuitos vecinos se eliminarán automáticamente de la unidad cuando desconecte parte de este bucle o red. Si desconectan la resistencia R1, automáticamente las demás resistencias dejarán de funcionar.
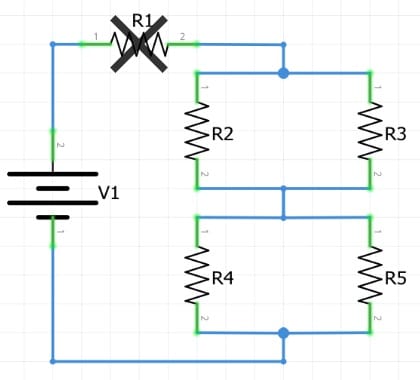
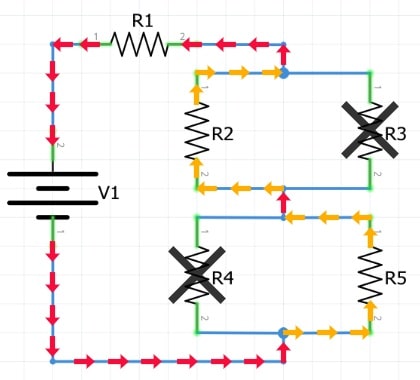
Por otro lado, en el caso de circuitos secundarios paralelos, si uno de los componentes se funde y se genera un punto abierto, la otra rama continuará operando independientemente.
Si se desconecta una de las resistencias en paralelo (R2, R3, R4 o R5), las ramas vecinas continuarán funcionando.
Aplicaciones
La gran mayoría de los electrodomésticos y dispositivos electrónicos se fabrican en base a circuitos mixtos.
Esto significa que los teléfonos móviles, computadoras, televisores, hornos de microondas y otros utensilios y aparatos similares tienen circuitos eléctricos mixtos como parte fundamental de sus conexiones internas.

Reducción (Ejemplos)
1.- Reducir el siguiente circuito mixto a una sola resistencia equivalente:
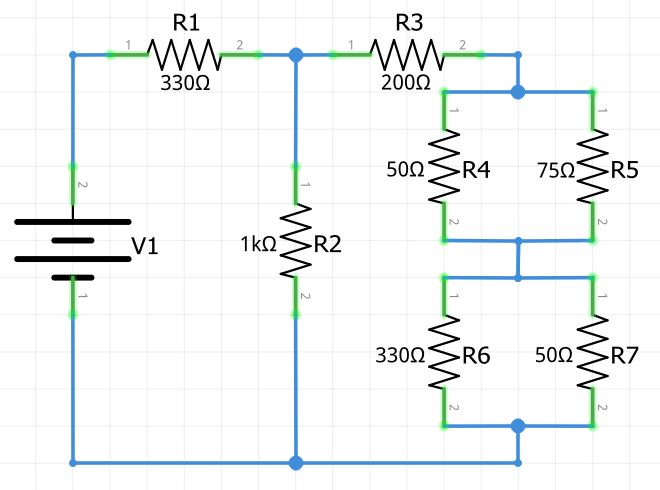
La mayoría de los circuitos mixtos son de esta forma. A pesar de que al principio parezca un circuito muy complejo y difícil de analizar, no tengas miedo de abordar estos circuitos en lo que respecta a los cálculos matemáticos.
Primero tienes que identificar las partes del circuito que están conectadas en serie y las que están en paralelo para poder aplicar selectivamente las reglas de serie y paralelo según sea necesario.
Una vez aplicadas estas reglas lograrás tener un circuito reducido y podrás determinar lo que está sucediendo con el voltaje, la intensidad, etc.
Es recomendable siempre iniciar la reducción de un circuito mixto desde el lado opuesto de la fuente de voltaje.
En este ejemplo se comenzará la reducción con las resistencias R6 y R7, que se encuentran conectadas en paralelo. Aplicando la fórmula de resistencia equivalente en circuitos en paralelo se obtiene lo siguiente:
R_{R_6||R_7}=\frac{1}{\frac{1}{R_6}+\frac{1}{R_7}}=\frac{1}{\frac{1}{330\Omega}+\frac{1}{50\Omega}}=\bold{43.421\Omega}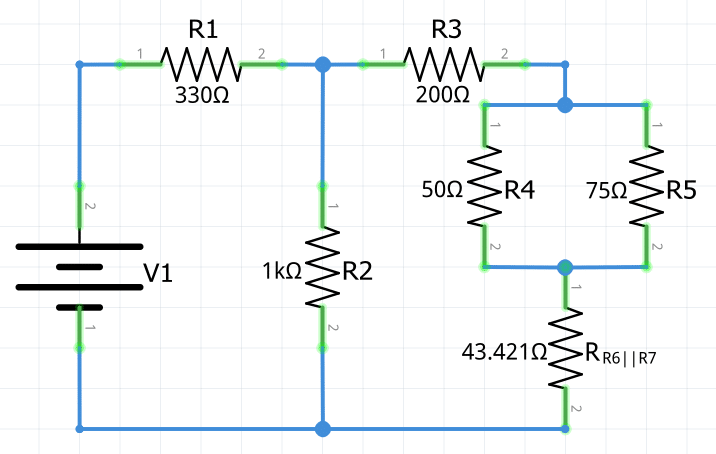
Repite el proceso anterior con las resistencias R4 y R5, que de igual manera se encuentran conectadas en paralelo. Aplicando la fórmula de resistencia equivalente en circuitos en paralelo se obtiene:
R_{R_4||R_5}=\frac{1}{\frac{1}{R_4}+\frac{1}{R_5}}=\frac{1}{\frac{1}{50\Omega}+\frac{1}{75\Omega}}=\bold{30\Omega}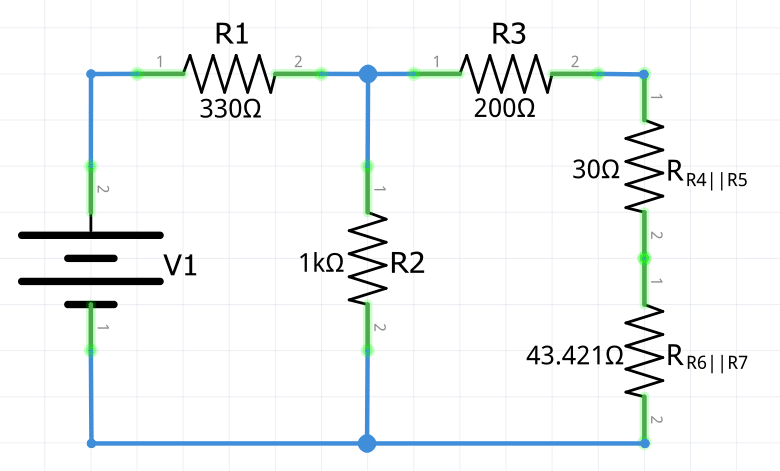
Ahora se encuentran tres resistencias en serie (la resistencia R3, la resistencia de 30Ω y la resistencia de 43.421Ω), por lo que se procede a simplificarlas.
Aplicando la fórmula de resistencia equivalente en circuitos en serie se tiene la siguiente expresión:
R_3+R_{R_4||R_5}+R_{R_6||R_7}=200\Omega+30\Omega+43.421\Omega=\bold{273.421\Omega}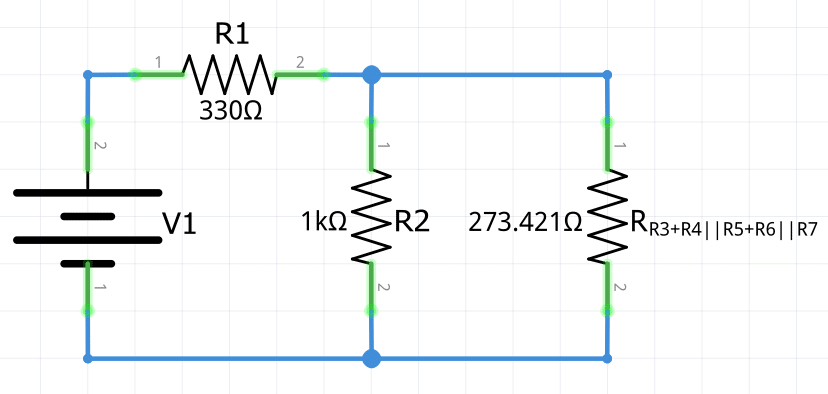
Un patrón está surgiendo. Se está trabajando en el esquema del circuito de derecha a izquierda, simplificando y volviéndolo a dibujar a medida que se avanza.
A continuación aparecen dos resistencias en paralelo, la resistencia R2 y la resistencia de 273.421Ω. Entonces se tiene la siguiente expresión matemática:
R_2||R_{(R_3+R_4||R_5+R_6||R_7)}=\frac{1}{\frac{1}{1000\Omega}+\frac1{273.421\Omega}}=\bold{214.714\Omega}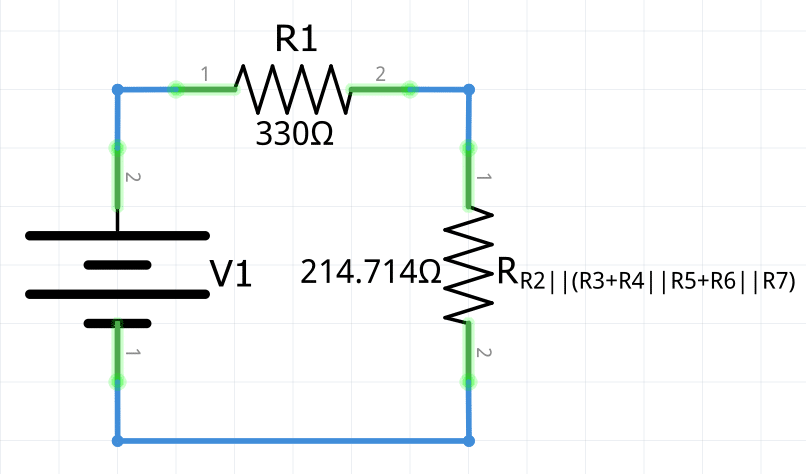
Únicamente quedan dos resistencias en serie. Sumando la resistencia de 214.714Ω con la resistencia R1 se tendrá la resistencia equivalente:
R_{eq}=R_1+R_{[R_2||(R_3+R_4||R_5+R_6||R_7)]}R_{eq}=330\Omega+214.714\Omega=\bold{544.714\Omega}De esta manera se llega a la resistencia equivalente en un circuito mixto.

Como conclusión se puede decir que si eres capaz de identificar qué partes del circuito están en serie y qué partes están en paralelo, podrás analizarlo por etapas, acercándose a cada parte de una en una, utilizando las reglas apropiadas para determinar la resistencia equivalente.
Análisis de circuito mixto Ejercicios resueltos paso a paso
1.- Determinar todas las caídas de voltaje, corrientes y resistencia total del siguiente circuito:
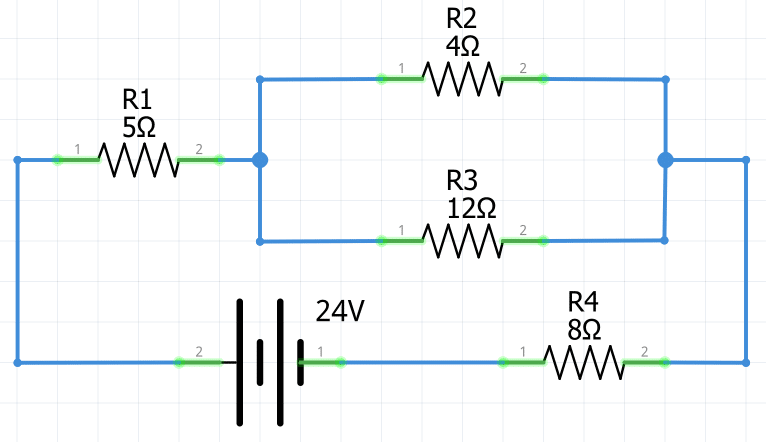
Resistencia total o equivalente
1 Primero tendrás que identificar qué partes del circuito están conectadas en serie y qué partes en paralelo, luego aplicar selectivamente las reglas de serie y paralelo según sea necesario para reducirlo y determinar lo que está sucediendo.
Se comienza con R2 y R3, que se encuentran conectadas en paralelo. Aplicando la fórmula de resistencia equivalente en circuitos en paralelo se obtiene lo siguiente:
R_{R_2||R_3}=\frac{1}{\frac{1}{R_2}+\frac{1}{R_3}}=\frac{1}{\frac{1}{4\Omega}+\frac{1}{12\Omega}}=\bold{3\Omega}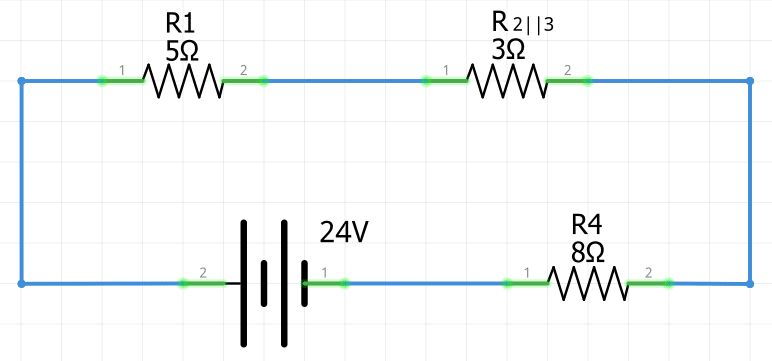
Una vez reducida la sección del circuito que estaba conectado en paralelo (R2 y R3), se aplica la fórmula de resistencia equivalente en serie con R1 y R4 como se muestra a continuación:
R_{eq}=R_1+R_{R_2||R_3}+R_4=5\Omega+3\Omega+8\Omega=\bold{16\Omega}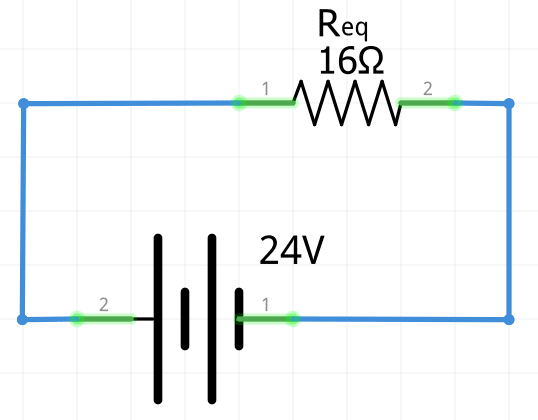
Intensidad total
2 Ahora deberás utilizar la ecuación de la ley de Ohm para determinar la corriente total en el circuito. Por lo tanto, es necesario usar la resistencia equivalente y el voltaje total (voltaje de la batería).
V_f=I_t\cdot R_{eq}Despejando la corriente total se llega al siguiente resultado:
I_t=\frac{V_{f}}{R_{eq}}=\frac{24V}{16\Omega}=\bold{1.5 A}Intensidades de las resistencias en serie
3 El cálculo actual de 1.5A representa la corriente en la ubicación de la batería. Sin embargo, las resistencias R1 y R4 están en serie y la corriente en las resistencias conectadas en serie es la misma en todas partes, así que:
I_t=I_{1}=I_{4}=\bold{1.5A}Caída de voltaje de resistencias en serie
4 Para ramas paralelas, la suma de la corriente en cada rama individual es igual a la corriente fuera de las ramas. Por lo tanto, I2 + I3 debe ser igual a 1.5A. La rama con la menor resistencia tendrá la mayor corriente. Determinar la cantidad de corriente requerirá que se utilice nuevamente la ecuación de la ley de Ohm. Pero para usarla, primero se debe conocer la caída de voltaje en las ramas.
Para determinar la caída de voltaje en las ramas paralelas, primero debe determinarse la caída de voltaje en cada una de las dos resistencias en serie (R1 y R4). La ecuación de la ley de Ohm se puede utilizar para determinar la caída de voltaje en cada resistencia. Estos cálculos se aprecian a continuación:
V_{1}=I_{1}\cdot R_1=1.5A\cdot 5\Omega=\bold{7.5V}V_{4}=I_{4}\cdot R_4=1.5A\cdot 8\Omega=\bold{12V}Voltaje de las resistencias en paralelo
5 Este circuito está alimentado por una fuente de 24 volts. Por lo tanto, habrá una caída de 19.5 V (7.5 V + 12 V) como resultado del paso a través de las dos resistencias conectadas en serie (R1 y R4). La caída de voltaje en las ramas debe ser de 4.5V para compensar la diferencia entre el total de 24V y la caída de 19.5V en R1 y R4, como se muestra a continuación:
V_{paralelo}=V_{2}=V_{3}Por lo tanto:
V_f=V_{1}+V_{paralelo}+V_{4}V_{paralelo}=V_f-V_{1}-V_{4}Sustituyendo los valores que ya conoce se obtiene el valor de la caída de voltaje en las ramas en paralelo:
V_{paralelo}=V_{2}=V_{3}=(24V-7.5V-12V)=\bold{4.5V}Corriente de las resistencias en paralelo
6 Ahora que ya conoces la caída de voltaje a través de las resistencias conectadas en paralelo (R1 y R4) utiliza la ecuación de la ley de Ohm para determinar la corriente en las dos ramas:
I_2=\frac{V_{2}}{R_2}=\frac{4.5V}{4\Omega}=\bold{1.125A}I_3=\frac{V_{3}}{R_3}=\frac{4.5V}{12\Omega}=\bold{0.375A}Resumen
El análisis ahora está completo y los resultados se resumen en la siguiente tabla:
| Req = | 16Ω | It = | 1.5A |
| I1 = | 1.5A | V1 = | 7.5V |
| I2 = | 1.125A | V2 = | 4.5V |
| I3 = | 0.375A | V3 = | 4.5V |
| I4 = | 1.5A | V4 = | 12V |
Pasos para el Análisis de un Circuito Mixto
- Identifica conexiones en serie y paralelo
Primero identifica qué partes del circuito están conectadas en serie y qué partes en paralelo
- Obtén la Resistencia Equivalente
Luego aplica selectivamente las reglas de serie y paralelo según sea necesario para reducirlo a una sola resistencia equivalente
- Calcula la Intensidad Total
Ahora usa la ecuación de la ley de Ohm para determinar la corriente total en el circuito
- Intensidades de las resistencias en serie
Una vez obtenida la Intensidad Total, encuentra las resistencias que estén en serie con la fuente de alimentación. La corriente en las resistencias conectadas en serie es la misma en todas partes
- Caída de voltaje de resistencias en paralelo
Para ramas conectadas en paralelo, la suma de la corriente en cada rama individual es igual a la corriente fuera de las ramas
- Voltaje de las resistencias en paralelo
Dependiendo de tu circuito, habrá una caída de voltaje como resultado del paso a través de resistencias conectadas en serie
- Intensidad de las resistencias en paralelo
Ahora que ya conoces la caída de voltaje a través de las resistencias conectadas en paralelo, utiliza la ecuación de la ley de Ohm para determinar la corriente en las dos ramas
Submit your review | |
Me gusto la información es interesante como puedes hacer que con palabras escritas se haga entendible, esta excelente. Pero también quiero aportar un granito de arena y por ello hice un video de cómo resolver un CIRCUITO MIXTO solo con la LEY DE OHM, LINK: https://youtu.be/CNTXIrL4SXY
la mejor explixación incluso mejor que mi profesor que e visto me ayudo muchisimo
excelente gracias
Excelente pagina, siempre me ayuda en mis trabajos
Excelente explicación, mil gracias!
Análisis de circuitos Circuito mixto Circuitos Circuitos básicos Electrónica y electricidad Introducción análisis de circuitos







13 comentarios
Gracias por su información me fue muy útil
Muy muy buena la explicación, la verdad es genial de que se puedan publicar estas cosa , por que nunca tenemos que dejar de estudiar y de aprender, voy a recomendar con mucho gusto está página por que se lo merece y por que ayuda y incentiva al aprendizaje
me ayudan con este, es encotrar la resistencia total del circuito mixto
R1=.234567 MΩ
R2=.631 KΩ
R3=1234 Ω
R4=735 KΩ
R5=538 Ω
Depende de como vallan conectados , si R1 o R2 , etc… van en serie o paralelo , dime y te lo resolvere entre 4-5 min
Hola, el circuito cómo sería desarrollado en la página Tinkercard? Es para un trabajo, pero medio entiendo.
excelente gracias
me llega
Excelente
Está muy completo la información , la verdad me ayudó mucho gracias por compartirlo
¡Gracias por tu comentario! Esperamos que sigas disfrutando de nuestro contenido.
Muchas gracias por la información 🙂
Agradecemos mucho tu comentario ¡Esperamos leerte
más seguido!
Oye gracias por la información es completa y verás , me fue de mucha utilidad!!!