Conductancia eléctrica

Se le denomina conductancia a la facilidad de que tiene un material al paso de la corriente eléctrica. Esta propiedad se es más notoria en los metales. Se puede deducir que la conductancia es el recíproco a la resistencia en un circuito.

Unidades

Fórmula

Para un elemento conductor, la resistencia eléctrica (R) y la conductancia eléctrica (G) se definen como:

\large\bold{G=\frac{1}{R}=\frac{I}{V}}

Donde G se llama conductancia

De este modo, se demuestra que una resistencia de 100Ω tiene un valor de conductancia igual a 1/100Ω=0.01S.

G=\frac{1}{R}

0.01S=\frac{1}{100\Omega}

Demostración de la fórmula

Recordando que por ley de Ohm, la resistencia es igual a voltaje sobre intensidad.

R=\frac{V}{I}

 Y como la conductancia es el inverso a la resistencia. Tomando como (1/R)=G entonces se tiene la siguiente expresión:

\frac{1}{R}=\frac{I}{V}

Se puede deducir que conductancia (G) es igual a intensidad sobre voltaje.

G=\frac{I}{V}

Por lo tanto, de igual manera es posible decir que conductancia es el recíproco de la resistencia.

G=\frac{1}{R}

Conductancia equivalente

Para calcular la conductancia equivalente de un circuito se utiliza el inverso de las fórmulas de resistencia equivalente, es decir, la conductancia en paralelo es una suma de cada conductancia, mientras que en serie es la suma algebraica de los inversos multiplicativos.

Circuitos en Serie

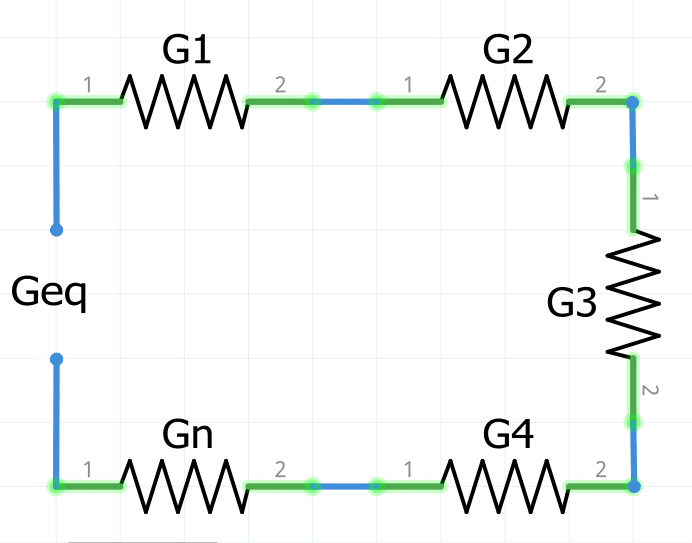
\large\bold{\frac1{G_{eq}}=\frac1{G_{1}}+\frac1{G_{2}}+\frac1{G_{3}}+\frac1{G_{4}}+...+\frac1{G_{n}}}

Circuitos en Paralelo

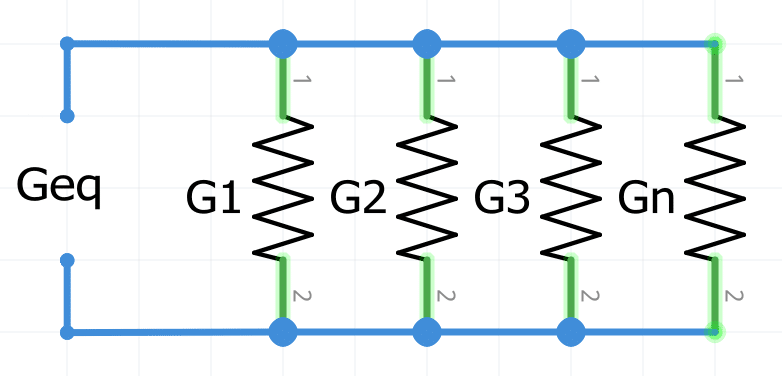
\large\bold{G_{eq}=G_1+G_2+G_3+...+G_n}

Ejercicios resueltos de conductancia equivalente en circuitos Mixtos

1.- Obtener la conductancia equivalente Geq del circuito que se muestra a continuación:

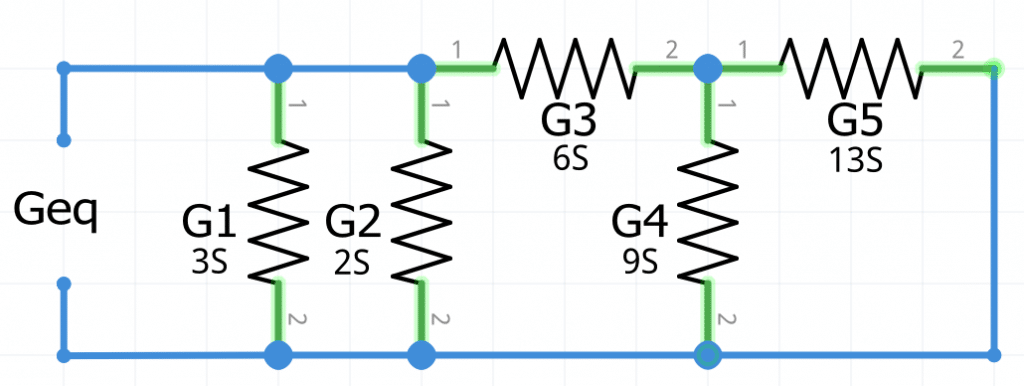
Es importante, siempre que sea posible, iniciar la reducción del circuito mixto desde el lado opuesto de la fuente de voltaje o de la Geq.

Primero las conductancias G4 y 5, que se encuentran conectadas en paralelo. Aplicando la fórmula de conductancia equivalente en circuitos paralelos se obtiene lo siguiente:

G_{G_4||G_5}=G_6=13S+9S=\bold{22S}

Ahora se encuentran dos conductancias en serie, por lo que se procede a simplificarlas (G3 y G6). Aplicando la fórmula de conductancia equivalente en circuitos en serie se tiene la siguiente expresión:

G_3+G_6=G_7=\frac{1}{\frac{1}{6S}+\frac{1}{22S}}=\bold{\frac{33}{7}S}

Únicamente quedan tres conductancias en paralelo. Sumando las conductancias G1, G2 y G7, finalmente se obtendrá la conductancia equivalente:

G_{eq}=G_1+G_2+G_7=3S+2S+\frac{33}{7}S=\large\bold{9.7142S}