Teorema de Thévenin y Norton

Los circuitos equivalentes de Thévenin y Norton son métodos básicos para analizar circuitos de Corriente Alterna y Corriente Directa. Es importante comprender los pasos necesarios para convertir un circuito a su equivalente de Thévenin o de Norton, pero lo más importante es comprender cómo estas técnicas pueden ayudarlo a analizar y diseñar dispositivos electrónicos reales.

Introducción

El teorema de Norton para circuitos eléctricos es dual del teorema de Thévenin.

Teorema de Thévenin

En términos prácticos, este teorema establece que se puede sustituir el circuito por una fuente de voltaje y una impedancia o resistencia conectados en serie.

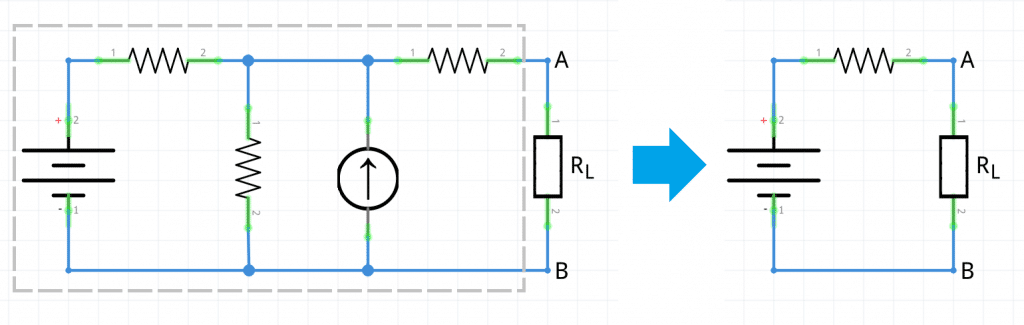
Corriente Directa DC

En corriente directa (DC), el teorema de Thévenin establece que cualquier red lineal (con dos fuentes independientes) puede ser reemplazada respecto a dos terminales A y B por un circuito equivalente que conste de una fuente de voltaje (V_Th ) conectada en serie con una resistencia (R_Th ).

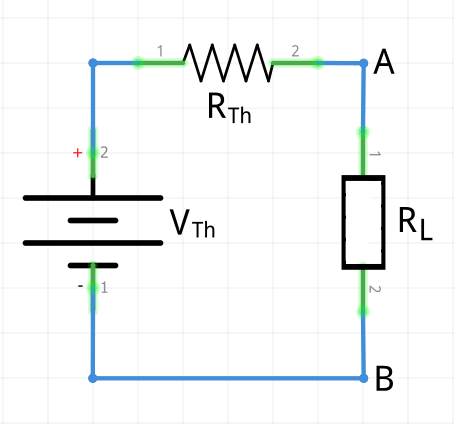
Cálculo de la tensión de Thévenin

Para calcular la tensión de Thévenin, V_Th , se desconecta la carga (es decir, la resistencia de la carga o R_L ) y se calcula V_AB . Al desconectar la carga, la intensidad que atraviesa R_Th en el circuito equivalente es nula y por tanto la tensión de R_Th también es nula. Por lo que ahora V_AB = V_Th por la segunda ley de Kirchhoff.

V_{AB}=V_{Th}

Debido a que la tensión de Thévenin se define como la tensión que aparece entre los terminales de la carga cuando se desconecta la resistencia de la carga, también se puede denominar tensión en circuito abierto.

V_{AB}=V_{Th}=V_{circuito\space abierto}

Cálculo de la resistencia de Thévenin

Para calcular la resistencia de Thévenin, se desconecta la resistencia de carga, se cortocircuitan las fuentes de tensión y se abren las fuentes de corriente. Se calcula la resistencia que se ve desde los terminales AB y esa resistencia R_AB es la resistencia de Thevenin buscada.

R_{Th}=R_{AB}

Corriente Alterna AC

En corriente alterna (AC), El teorema de Thévenin establece que en un circuito con dos terminales se puede sustituir por otro sencillo que consta de un generador de corriente alterna (V_Th ) y una impedancia en serie (Z_Th ).

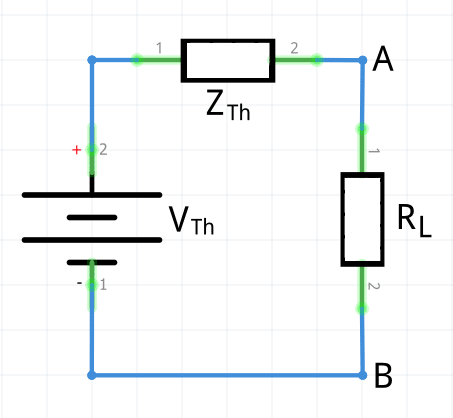
Cálculo del voltaje de Thévenin

Al igual que en corriente directa, para calcular el voltaje de Thévenin, V_Th , se debe desconectar la carga (R_L ) y se calcula el voltaje entre las terminales A y B (V_AB ). Al desconectar la carga, la intensidad que atraviesa R_Th en el circuito equivalente es nula y por tanto la tensión de R_Th también es nula.

V_{AB}=V_{Th}

Ya que el Voltaje de Thévenin se define como el voltaje existente entre los terminales A y B cuando se desconecta la resistencia de la carga, también se puede denominar Voltaje en circuito abierto.

V_{AB}=V_{Th}=V_{circuito\space abierto}

Cálculo de la impedancia de Thévenin

Para calcular la impedancia de Thévenin Z_Th , se desconecta la resistencia de carga, se cortocircuitan las fuentes de voltaje y se abren las fuentes de corriente. Se calcula la impedancia que se ve desde los terminales AB y esa impedancia Z_AB es la impedancia de Thevenin buscada.

Z_{Th}=Z_{AB}

Thévenin Ejercicios resueltos paso a paso

1.- Encuentre el equivalente de Thévenin del siguiente circuito.

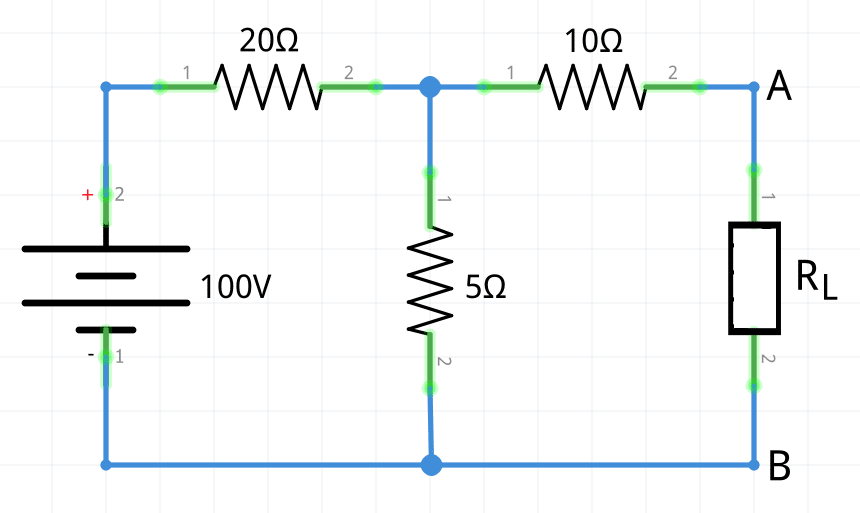
1 En primer lugar se calcula el voltaje de Thévenin entre los terminales A y B de la carga; para ello, se desconecta R_L del circuito (queda un circuito abierto entre A y B). Una vez hecho esto, se puede observar que la resistencia de 10 Ω está en circuito abierto y no circula corriente a través de ella, con lo que no produce ninguna caída de tensión.

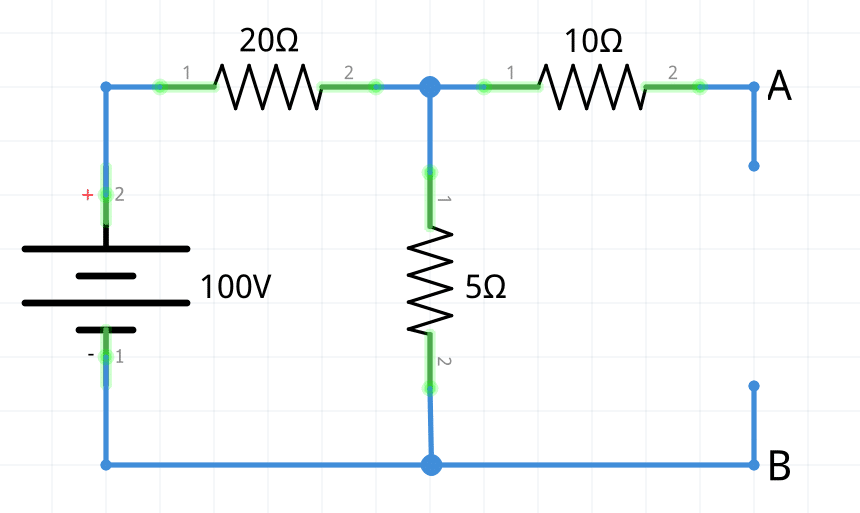
En estos momentos, el circuito que se necesita estudiar para calcular la tensión de Thévenin está formado únicamente por la fuente de tensión de 100 V en serie con dos resistencias, una de 20 Ω y otra de 5 Ω.

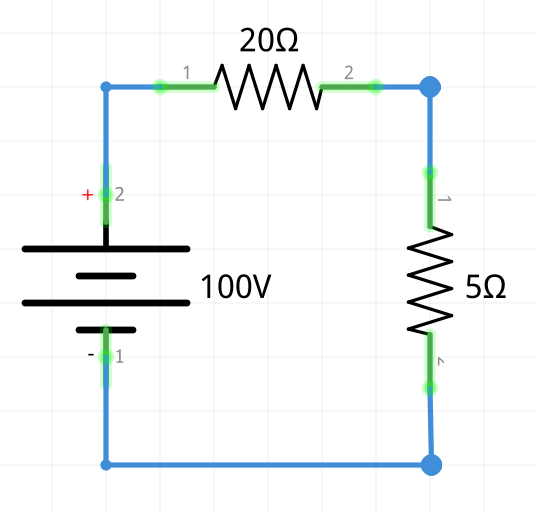
Como la carga R_L está en paralelo con la resistencia de 5 Ω, la diferencia de potencial entre los terminales A y B es igual que la tensión que cae en la resistencia de 5 Ω (ver también Divisor de tensión), con lo que la tensión de Thévenin resulta:

V_{Th}=\frac{5}{20+5}\cdot100V=\large\bold{20V}

2 Ahora se debe calcular la resistencia de Thévenin, para ello se desconecta la carga R_L del circuito y se anula la fuente de tensión sustituyendola por un cortocircuito. Por lo tanto, se halla la equivalente a las tres resistencias: las resistencias de 20 Ω y 5 Ω están conectadas en paralelo y estas están conectadas en serie con la resistencia de 10 Ω, entonces:

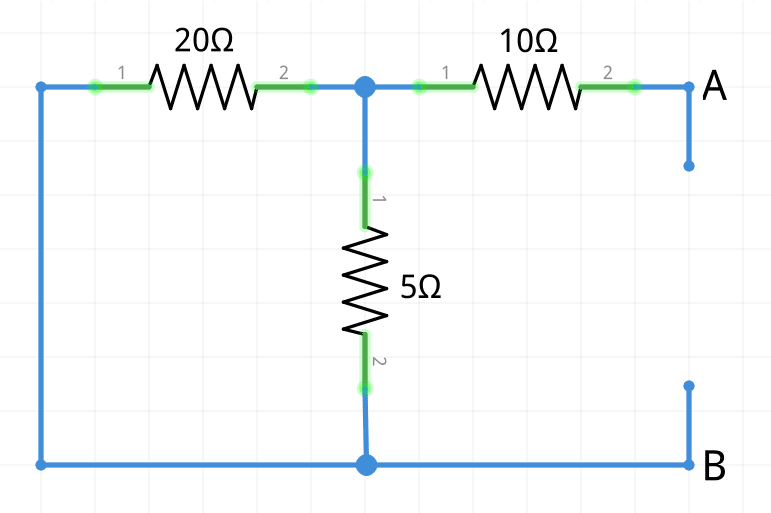
Por lo tanto, se halla la equivalente a las tres resistencias: las resistencias de 20 Ω y 5 Ω están conectadas en paralelo y estas están conectadas en serie con la resistencia de 10 Ω, entonces:

R_{Th}=\frac{20\cdot5}{20+5}+10\Omega=\large\bold{14\Omega}

3 Finalmente se redibuja el circuito sustituyendo todo con el equivalente Thévenin (V_Th y R_Th ); recordando que la fuente de tensión (voltaje de Thévenin) debe estar conectada en serie con la resistencia antes calculada (resistencia de Thévenin). Entonces, el circuito equivalente consiste en una fuente de tensión de 20V en serie con una resistencia de 14Ω.

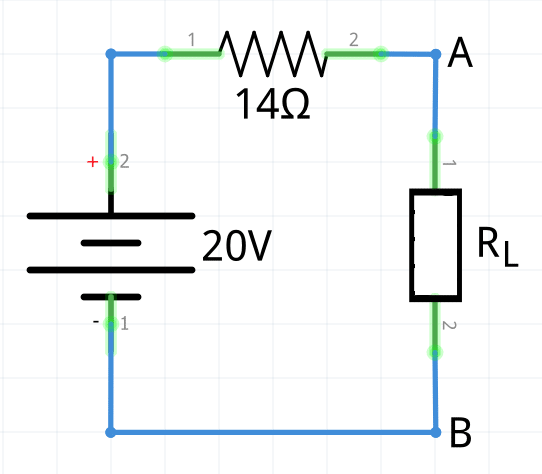
Teorema de Norton

En términos prácticos, este teorema establece que se puede sustituir el circuito por una fuente de corriente y una impedancia o resistencia conectados en paralelo.

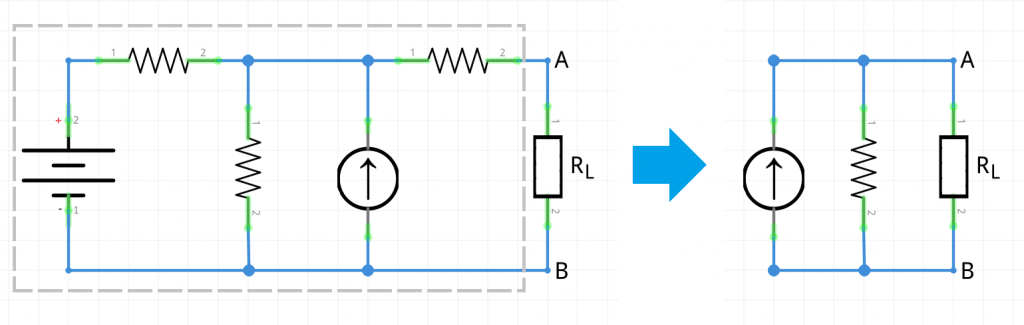
Corriente Directa DC

En corriente directa, el teorema de Norton establece que cualquier red de corriente directa lineal bilateral de dos terminales puede ser reemplazada por un circuito equivalente que consista de una fuente de corriente (I_N ) y una resistencia en paralelo (R_N ).

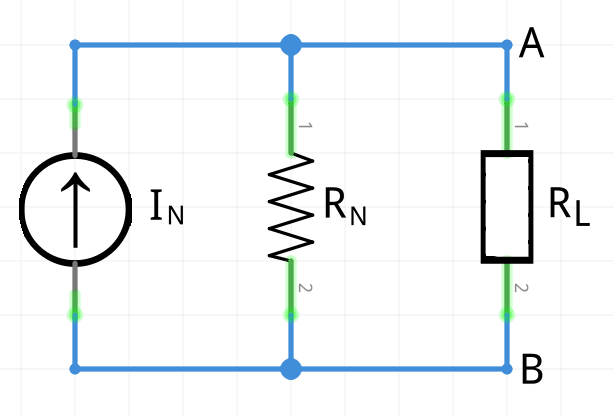
Al sustituir un generador de corriente por uno de tensión, el borne positivo del generador de tensión deberá coincidir con el borne positivo del generador de corriente y viceversa.

Cálculo de la corriente de Norton

Se calcula la corriente de salida, I_AB , cuando se cortocircuita la salida, es decir, cuando se pone una carga (tensión) nula entre A y B. Al colocar un cortocircuito entre A y B toda la intensidad I_N circula por la rama AB, por lo que ahora I_AB es igual a I_N .

I_{N}=I_{AB}

Cálculo de la resistencia de Norton

Se calcula la tensión de salida, V_AB , cuando no se conecta ninguna carga externa, es decir, cuando se pone una resistencia infinita entre A y B. R_N es ahora igual a V_AB dividido entre I_N porque toda la intensidad I_N ahora circula a través de R_N y las tensiones de ambas ramas tienen que coincidir.

R_N=\frac{V_{AB}}{I_N}

Corriente Alterna AC

En corriente alterna, el teorema de Norton establece que cualquier circuito lineal se puede sustituir por una fuente equivalente de corriente (I_N ) en paralelo con una impedancia equivalente (Z_N ).

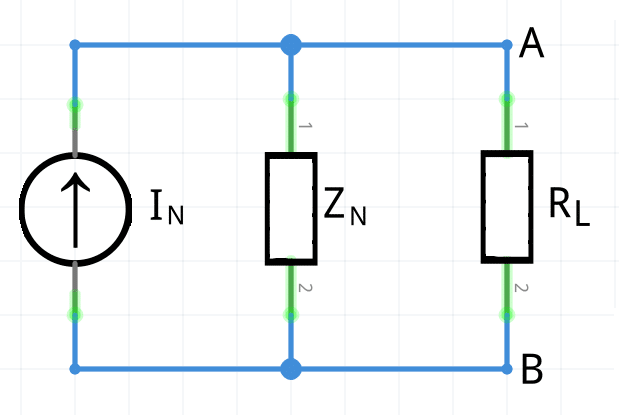
Al sustituir un generador de corriente por uno de tensión, el borne positivo del generador de tensión deberá coincidir con el borne positivo del generador de corriente y viceversa.

Cálculo de la impedancia de Norton

Se calcula la tensión de salida, V_AB , cuando no se conecta ninguna carga externa, es decir, cuando se pone una resistencia infinita entre A y B. Z_N es ahora igual a V_AB dividido entre I_N porque toda la intensidad I_N ahora circula a través de Z_N y las tensiones de ambas ramas tienen que coincidir.

Z_N=\frac{V_{AB}}{I_N}

Teorema de Norton Ejercicios resueltos paso a paso

1.- Encontrar el equivalente de Norton del siguiente circuito.

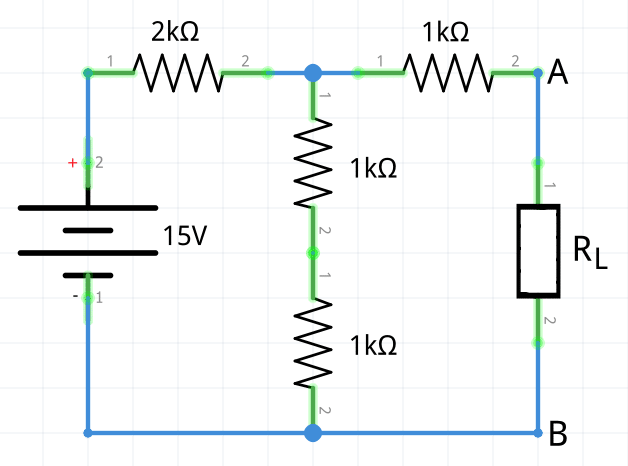
1 En primer lugar se calcula la corriente de Norton entre los terminales A y B de la carga; para ello, se desconecta R_L del circuito (queda un circuito abierto entre A y B). Una vez hecho esto, se procede a obtener la intensidad total que viene dada por:

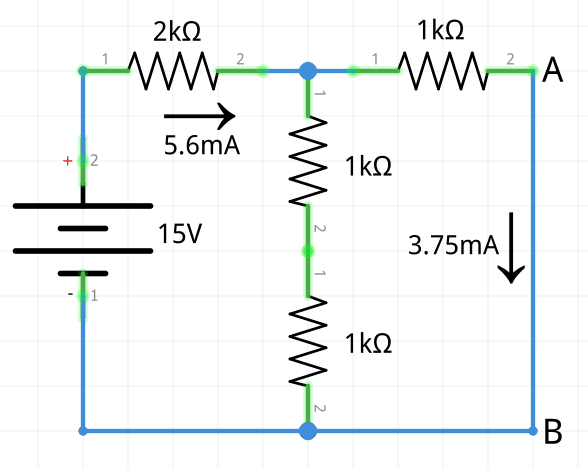
I_{total}=\frac{15V}{2k\Omega+(1k\Omega||(1k\Omega+1k\Omega))}=\bold{5.625mA}

Utilizando la regla del divisor de corriente se puede obtener la intensidad entre las terminales A y B.

I_N=\frac{1k\Omega+1k\Omega}{(1k\Omega+1k\Omega+1k\Omega)}\cdot I_{total}=\large\bold{3.75mA}

2 Ahora se debe calcular la resistencia de Norton, para ello se desconecta la carga R_L del circuito y se anula la fuente de voltaje sustituyendola por un cortocircuito. Por lo tanto, se halla la equivalente a las cuatro resistencias: las resistencias centrales de 1kΩ están conectadas en serie, éstas a su vez están conectadas en paralelo con la resistencia de 2kΩ para finalmente estar conectadas en serie con la resistencia de 1kΩ que se encuentra del lado derecho, entonces:

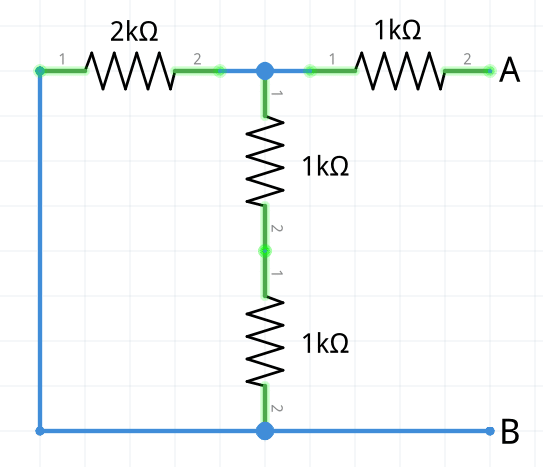
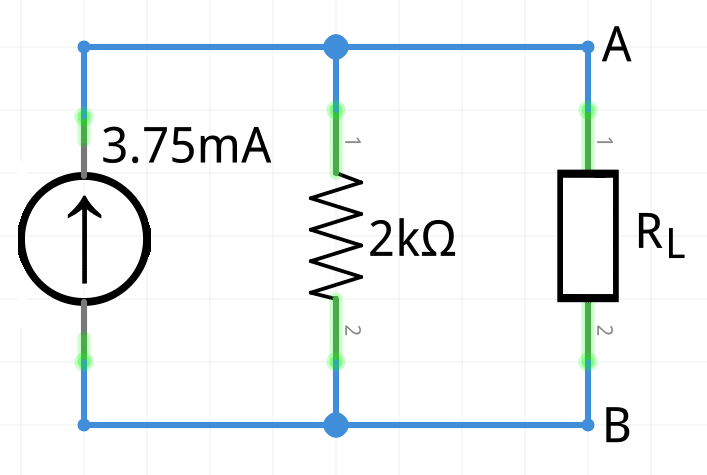
R_N=1k\Omega+(2k\Omega||(1k\Omega+1k\Omega))=\large\bold{2k\Omega}

3 Finalmente se redibuja el circuito sustituyendo todo con el equivalente Norton (I_N y R_N ); recordando que la fuente de corriente (corriente de Norton) debe estar conectada en paralelo con la resistencia antes calculada (resistencia de Norton). Por lo tanto, el circuito equivalente consiste en una fuente de intensidad de 3.75mA en paralelo con una resistencia de 2 kΩ.

Conversiones

Dado que los Teoremas de Thévenin y Norton son dos métodos igualmente válidos para reducir una red compleja a algo más simple de analizar, existe una forma de convertir el circuito equivalente de Thévenin en un circuito equivalente de Norton, y viceversa. El procedimiento es muy simple.

Es posible que haya notado que el procedimiento para calcular la resistencia de Thévenin es idéntico al procedimiento para calcular la resistencia de Norton: elimina todas las fuentes de energía y determina la resistencia entre los puntos de conexión de carga abierta. Como tal, las resistencias de Thévenin y Norton para la misma red original deben ser iguales. Usando los circuitos de ejemplo de las dos últimas secciones, se puede observar que las dos resistencias son iguales:

R_{Thevenin}=R_{Norton}

Pasar de Thévenin a Norton

En caso de que se quisiera convertir el circuito equivalente de Thévenin al circuito equivalente de Norton, se puede decir que por Ley de Ohm la corriente de Norton es lo mismo que el voltaje de Thévenin dividida entre la resistencia Thévenin:

R_N=R_{Th}

I_N=\frac{V_{Th}}{R_{Th}}

Pasar de Norton a Thévenin

Si quisiera convertir el circuito equivalente de Norton al circuito equivalente de Thévenin, se podría usar la misma resistencia y calcular el voltaje de Thévenin con la Ley de Ohm.

R_{Th}=R_N

V_{Th}=I_N\cdot R_N

Estas equivalencias entre los circuitos de Thévenin y Norton pueden ser una herramienta útil que debes tener presente a futuro.