Teorema de Nodos

Definición de Nodo en circuitos eléctricos

Un nodo es cualquier punto en un circuito donde se encuentren conectados dos o más componentes. A continuación se muestra un circuito formado por 4 nodos. Cada nodo se representa con un color diferente.

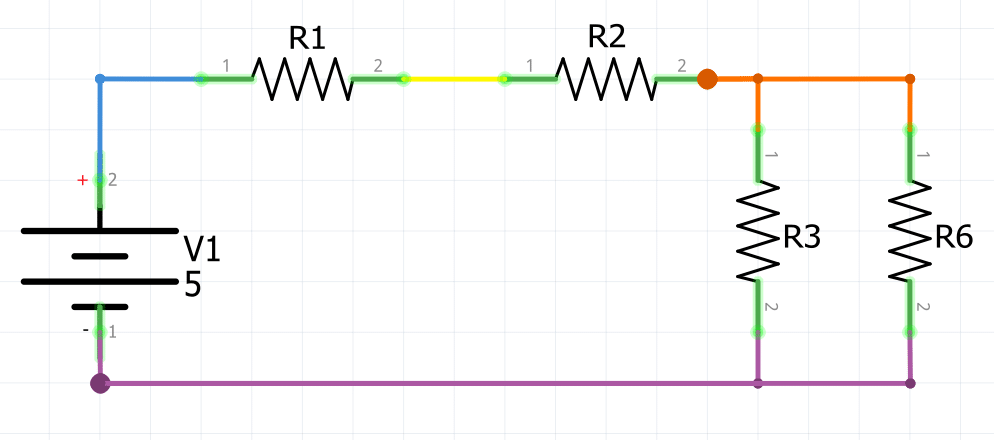
Para el análisis de cualquier circuito electrónico, las corrientes que «salen» del nodo son positivas, mientras que las que «entran» son negativas.

Primera Ley de Kirchhoff

La definición de la primera ley de Kirchhoff es la siguiente:

Las corrientes de entrada de un nodo son iguales a la suma de las corrientes de salida.

Por lo tanto, durante el análisis nodal en cada punto de un nodo se debe escribir la primera ecuación de la ley de Kirchhoff y luego expresar cada corriente en términos del voltaje a través de la rama.

Pasos del Teorema de Nodos

Ejemplos paso a paso

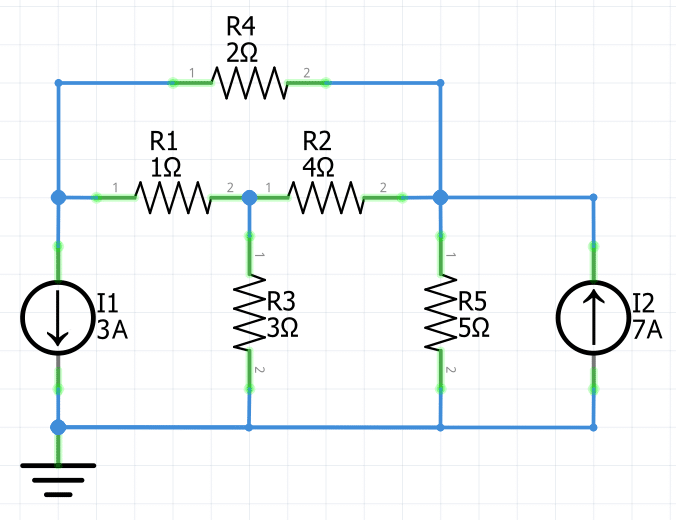
1.- Calcula el voltaje en cada fuente de corriente del siguiente circuito.

Nodo de referencia

1 Se explicarán y aplicarán los pasos antes mencionados. El primer paso del análisis nodal es seleccionar un nodo como nodo de referencia o de base. El nodo de referencia se llama comúnmente tierra, pues se supone que tiene potencial cero (v=0). En este ejemplo se tienen un total de 4 nodos. Se eligió el nodo inferior como nodo de referencia.

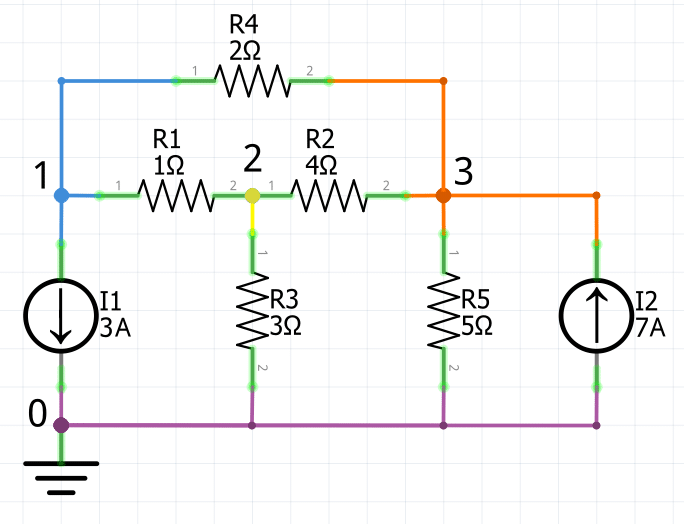
El nodo 0 es el nodo de referencia (v = 0), mientras que a los nodos 1, 2 y 3 se les asignan las tensiones v1, v2 y v3, respectivamente.

Téngase en cuenta que las tensiones de los nodos se definen respecto al nodo de referencia. Cada voltaje de nodo es la evaluación de la tensión respecto al nodo de referencia desde el nodo correspondiente.

Ahora se asignan las tensiones v1, v2, . . . , v(n–1), a los nodos restantes. En este ejemplo se etiquetan los voltajes v1, v2 y v3.

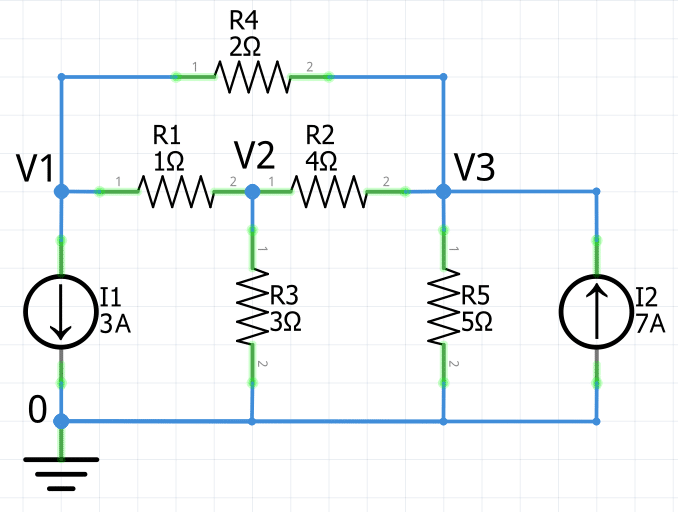
Dibujar trayectoria de las corrientes

2 Para facilitar el análisis por el teorema de nodos deberás trazar las trayectorias de las corrientes en cada rama (en caso de que no estén especificadas). Para este ejemplo únicamente se especifican las direcciones de dos trayectorias: las corrientes de las fuentes I1 e I2. Entonces se deben dibujar las direcciones de las corrientes restantes (en este caso I1, I2, I3, I4 e I5).

Puedes elegir cualquier dirección para las corrientes no especificadas, pero tratando de trazar trayectorias que vayan hacia el nodo de referencia.

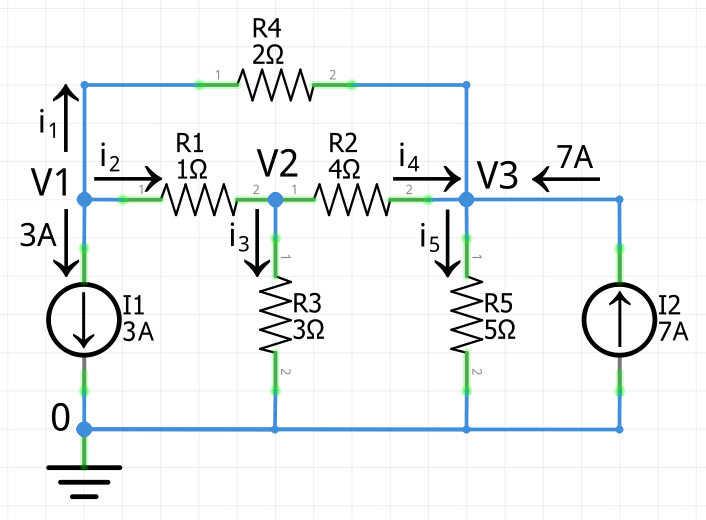
Aplicar ley de corrientes de Kirchhoff

3 Como tercer paso se aplica la Ley de Corrientes de Kirchhoff a cada nodo del circuito (excepto al de referencia).

Ecuación del primer nodo V1

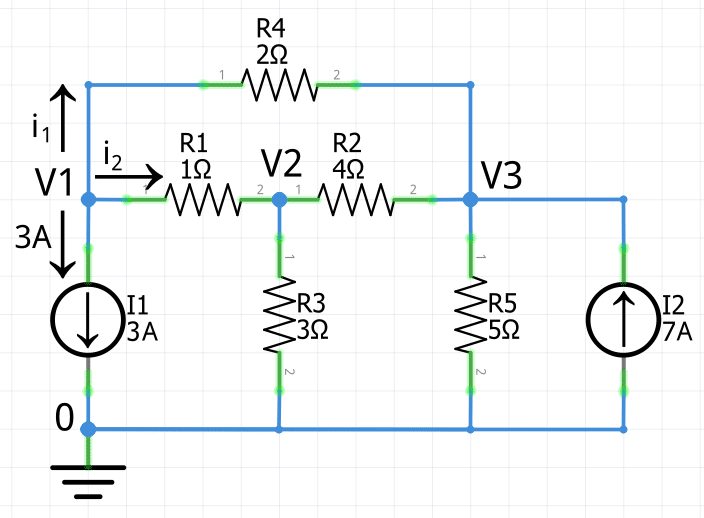
En el nodo 1, la aplicación de la Ley de Corrientes de Kirchhoff produce la siguiente ecuación:

3A+i_1+i_2=0

Usando la Ley de Ohm para expresar las corrientes i1 e i2 en términos de la tensión, la ecuación queda de la siguiente forma:

3A+\frac{V_1-V_3}{2\Omega}+\frac{V_1-V_2}{1\Omega}=0

Despejando y realizando el álgebra correspondiente se tiene:

\frac{V_1-V_3}{2\Omega}+\frac{V_1-V_2}{1\Omega}=-3A

\frac{V_1-V_3+2V_1-2V_2}{2}=-3

\bigg\lparen\frac{3V_1-V_3-2V_2}{2}=-3\bigg\rparen\cdot2

\large\bold{3V_1-2V_2-V_3=-6}

Ecuación del segundo nodo V2

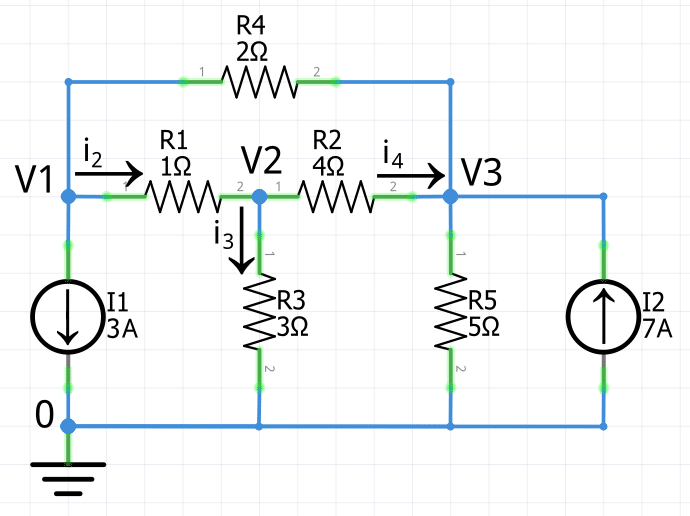
En el nodo 2, aplicando la Ley de Corrientes de Kirchhoff se obtiene la ecuación que se muestra a continuación:

-i_2+i_3+i_4=0

i_2=i_3+i_4

Una vez aplicada la Ley de Ohm para expresar las corrientes i2, i3 e i4 en términos de la tensión, se obtiene la siguiente expresión:

\frac{V_2-V_1}{1\Omega}=\frac{V_2-0}{3\Omega}+\frac{V_2-V_3}{4\Omega}

Despejando y realizando el álgebra correspondiente se tiene:

V_2-V_1=\frac{V_2}{3\Omega}+\frac{V_2-V_3}{4\Omega}

\bigg\lparen V_2-V_1=\frac{V_2}{3\Omega}+\frac{V_2-V_3}{4\Omega}\bigg\rparen\cdot12

12V_2-12V_1=4V_2+3V_2-3V_3

\large\bold{12V_1-5V_2-3V_3=0}

Ecuación del tercer nodo V3

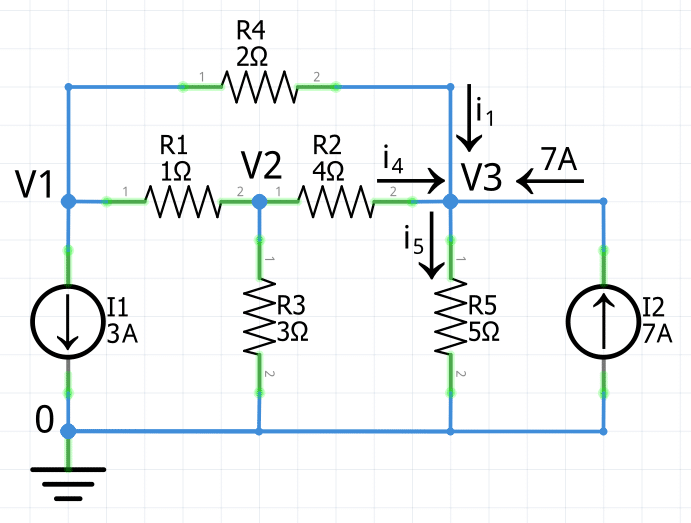
En el nodo 3, una vez que se aplica la Ley de Corrientes de Kirchhoff se obtiene la siguiente expresión:

-i_1-i_4+i_5-7A=0

i_5-i_4-i_1=7A

Usando la Ley de Ohm para expresar las corrientes i1 e i2 en términos de la tensión, la ecuación queda de la siguiente forma:

\frac{V_3-0}{5\Omega}-\frac{V_3-V_2}{4\Omega}-\frac{V_3-V_1}{2\Omega}=7A

Despejando y realizando el álgebra correspondiente se tiene:

\frac{V_3}{5\Omega}-\frac{V_3-V_2}{4\Omega}-\frac{V_3-V_1}{2\Omega}=7A

\frac{V_3}{5}-\frac{V_3-V_2}{4}-\frac{V_3-V_1}{2}=7

\bigg\lparen\frac{V_3}{5}-\frac{V_3-V_2}{4}-\frac{V_3-V_1}{2}=7\bigg\rparen\cdot20

4V_3-5V_3-5V_2-10V_3-10V_1=140

\large\bold{-10V_1-5V_2-11V_3=140}

Resolver sistema de ecuaciones

4 El cuarto paso del análisis nodal es resolver el sistema de ecuaciones con las ecuaciones obtenidas de cada nodo. Se aplicó la Ley de Corrientes de Kirchhoff a los n – 1 nodos de no referencia (v1, v2 y v3), y se obtuvieron 3 ecuaciones simultáneas.

El sistema de ecuaciones es el siguiente:

\begin{cases}
   3V_1-2V_2-V_3=-6 \\
   12V_1-5V_2-3V_3=0 \\
   -10V_1-5V_2-11V_3=140
\end{cases}

Para obtener las tensiones de los nodos v1, v2 y v3 puede utilizar cualquier método estándar para resolver sistemas de ecuaciones, como el método de sustitución, el método de eliminación, la regla de Cramer o la inversión de matrices. Para emplear alguno de los dos últimos métodos, las ecuaciones simultáneas deben enunciarse en forma matricial.

Los valores de las tensiones en cada nodo del circuito son:

\large\bold{\begin{cases}
   V_1=\frac{50}{47}V \\
   V_2=\frac{696}{47}V \\
   V_3=\frac{960}{47}V
\end{cases}}