Teorema de Mallas

Introducción al Análisis de Mallas

El procedimiento del análisis de mallas o teorema de mallas se basa en la Ley de Voltajes de Kirchhoff. Estrictamente se aplica en circuitos planos y en muchos casos puede resultar más fácil que el análisis de nodos. A continuación, se definirán los conceptos de malla y LVK ya que son fundamentales cuando se considera el análisis de mallas en un circuito.

Definición de Malla eléctrica

Una malla en electrónica es un camino cerrado que se conforma por componentes electrónicos, ya sean fuentes, resistencias, inductores, capacitores, etc.

A continuación se muestran dos ejemplos de circuitos formados por 4 mallas eléctricas.

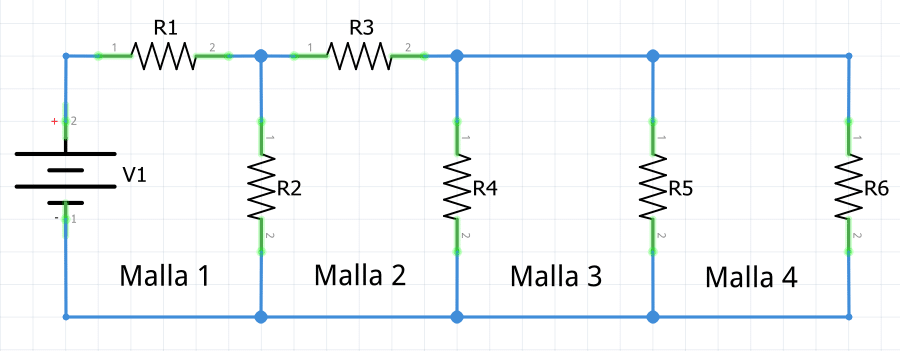
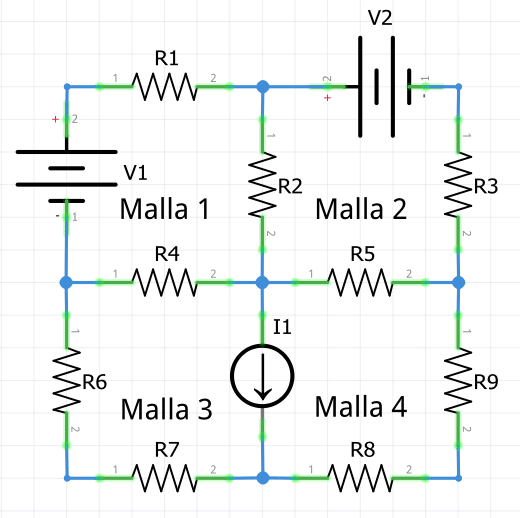
Ley de Voltajes de Kirchhoff

La Ley de voltajes de Kirchhoff indica que la suma de voltajes alrededor de una trayectoria o circuito cerrado debe ser igual a cero, por lo tanto en cada una de las mallas deberás obtener una ecuación conformada con los voltajes de los componentes igualada a cero.

Pasos Teorema de Mallas eléctricas

Ejercicios resueltos paso a paso

1.- Obtenga las corrientes que circulan en las mallas del siguiente circuito utilizando el Teorema de Mallas (o análisis de mallas).

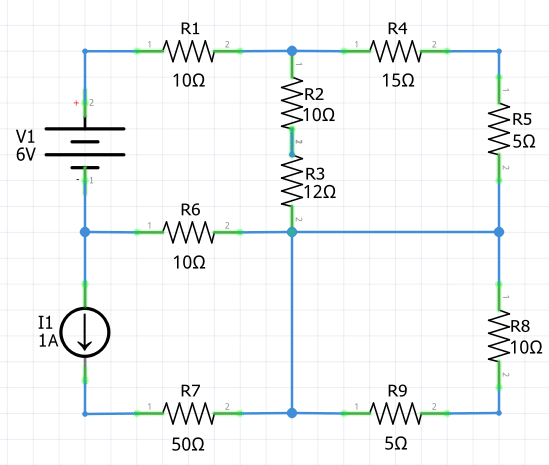
Identificar el número de mallas

1 Primero deberás identificar el número de mallas que tiene el circuito. A esta altura ya debes saber lo que es una malla eléctrica y cómo se identifican en cualquier circuito electrónico.

En este ejemplo, el circuito está conformado por un total de 4 mallas.

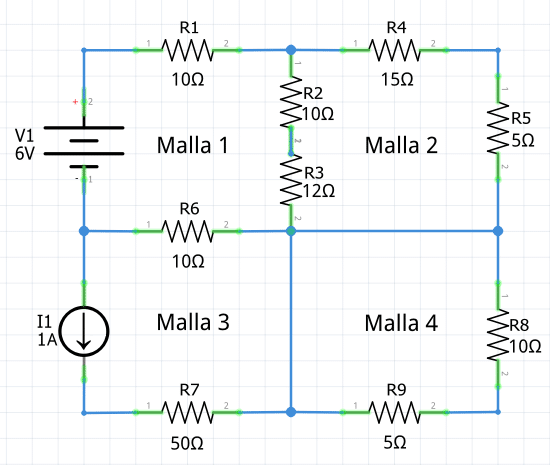
Nombrar y darle dirección a la intensidad de cada malla

2 Ahora, tendrás que nombrar y darle dirección a la intensidad de cada una de las mallas del circuito (I1, I2, I3, … ,In). Usualmente la dirección de la corriente se representa con una flecha que va en sentido horario, como se muestra a continuación con las cuatro intensidades del circuito:

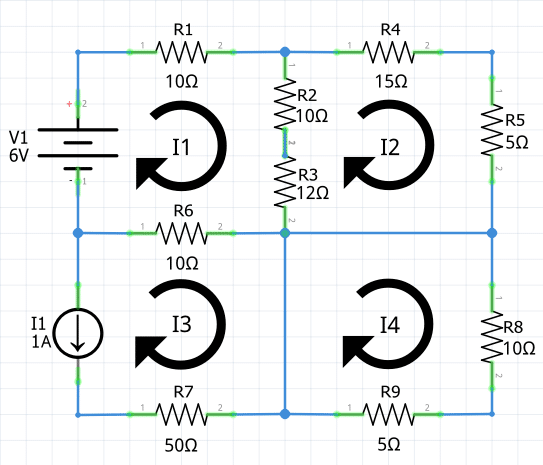
Se recomienda trabajar la dirección de cada malla en sentido horario (sentido en el que avanzan las manecillas del reloj).

Obtener las ecuaciones de cada malla

3 Ahora, obtendrás las ecuaciones de cada una de las mallas que, como establece la segunda ley de Kirchhoff, deben ser ecuaciones conformadas por la suma del voltaje de cada componente igualando a cero.

Ya que el circuito está conformado únicamente por resistencias (además de las fuentes de voltaje e intensidad), se usará como apoyo la ley de Ohm para encontrar los voltajes de estas resistencias.

La Ley de Ohm establece que el voltaje que se desea obtener, es igual al producto del valor de la resistencia por la intensidad de la malla:

V=RI

Por lo tanto, se multiplica el valor de las resistencias por el valor de la intensidad de corriente de cada malla del circuito.

Ecuación de la primera malla

Se irá obteniendo cada sumando de la ecuación (componente a componente) comenzando con la fuente de voltaje y avanzando en sentido a las manecillas del reloj.

El voltaje de la fuente es directamente 6V pero como el sentido que se está siguiendo entra por el lado negativo de la fuente. Entonces el primer sumando es -6.

\bold{-6}

Ahora va la resistencia R1 de 10Ω a la cual únicamente le está afectando la corriente I1 y por lo tanto, usando Ley de Ohm, el segundo sumando será (10Ω)(I1 A)= 10 I1.

-6\bold{+10I_1}

Luego toca la segunda resistencia R2 de 10Ω que en este caso está siendo afectada por I1 e I2.

Toma en cuenta que cuando dos corrientes están afectando una sola resistencia siempre se debe restar la corriente de la malla que se está analizando (en este caso I1), menos la corriente de la otra malla que afecta a la resistencia (en este caso la intensidad I2).

Por lo tanto, el tercer sumando es 10(I1-I2).

-6+10I_1\bold{+10(I_1-I_2)}

De igual forma la resistencia R3 de 12Ω está siendo afectada por I1 e I2.

Entonces, si se realiza el mismo proceso que con la resistencia anterior, el siguiente sumando será 12(I1-I2).

-6+10I_1+10(I_1-I_2)\bold{+12(I_1-I_2)}

El último elemento de la primera malla es la resistencia R6 de 10Ω que está siendo afectada por las corrientes de I1 e I3. Por lo tanto el último sumando será 10(I1-I3).

-6+10I_1+10(I_1-I_2)+12(I_1-I_2)\bold{+10(I_1-I_3)}

Finalmente se iguala la ecuación a cero (tomando en cuenta lo que nos dice la Ley de voltajes de Kirchhoff) y así se obtendrá la ecuación de la Malla 1.

\large\bold{-6+10I_1+10(I_1-I_2)+12(I_1-I_2)+10(I_1-I_3)=0}

Ecuación de la segunda malla

Se realiza el mismo proceso que con la Malla 1, comenzando desde la resistencia R3 de 12Ω y siguiendo también el sentido de las manecillas del reloj. Una vez hecho lo anterior se obtiene la siguiente ecuación:

\large\bold{12(I_2-I_1)+10(I_2-I_1)+15I_2+5I_2=0}

Como se puede observar, ya que la malla 2 tiene únicamente resistencias, se aplica la Ley de Ohm en cada una de estas para obtener los términos que conforman la ecuación.

Ecuación de la tercer malla

Ya que en el circuito se tiene únicamente una fuente de corriente que afecta a esta malla la corriente de la malla es igual al valor de la fuente de corriente, pero como dicha fuente va en dirección contraria a la I3, la ecuación de la Malla 3 queda de la siguiente manera:

\large\bold{I_3=-1A}

Ecuación de la cuarta malla

En esta malla hay dos resistencias a las cuales les afecta la intensidad 4 (I4), utilizando nuevamente la ley de ohm, la ecuación para la Malla 4 se muestra a continuación:

\large\bold{5I_4+10I_4=0}

Como se puede observar desde el diagrama del circuito, la Malla 4 está en corto y gracias a esto a las únicas resistencias que afectan esta malla nunca les va a llegar voltaje; por lo tanto en la Malla 4 no existe ninguna intensidad en (I4=0).

Establecer y resolver Sistema de Ecuaciones

4 Una vez obtenidas las 4 ecuaciones para las 4 mallas, se procede a reducirlas algebraicamente. Luego podrás resolver el sistema de ecuaciones. El sistema de ecuaciones que resulta en este caso es el siguiente:

\begin{cases}42I_1-22I_2-10I_3=6\\-22I_1+42I_2=0\\I_3=-1\\15I_4=0\end{cases}

Finalmente, con la ayuda de cualquier método para resolver sistemas de ecuaciones, se obtienen los siguientes resultados:

\large\bold{\begin{gathered}I_1=-131.25mA\\I_2=-68.75mA\\I_3=-1A\\I_4=0A
\end{gathered}}