Es una propiedad de los materiales que indica qué tanto se opone el material al flujo de corriente eléctrica. El valor de la resistividad es dependiente de la temperatura.
Las unidades en el S.I. de la resistencia específica (o resistividad) son el ohmio por metro (Ω·m).
Explicación simple de la resistencia específica
La resistencia eléctrica específica (o resistividad) es una constante de proporcionalidad que permite el cálculo de las resistencias eléctricas en función de sus dimensiones geométricas.
El valor de la resistividad depende, entre otras cosas, del material de la resistencia eléctrica y su temperatura.
En este sentido, la resistividad es una constante dependiente de la temperatura, lo que significa que un material no tendrá la misma resistividad a 20°C que a 25°C.
La relación entre la resistencia eléctrica de un conductor por un lado y sus dimensiones geométricas por otro lado está mediada por la resistividad.
Fórmula
La relación entre la resistencia eléctrica y las dimensiones geométricas es:
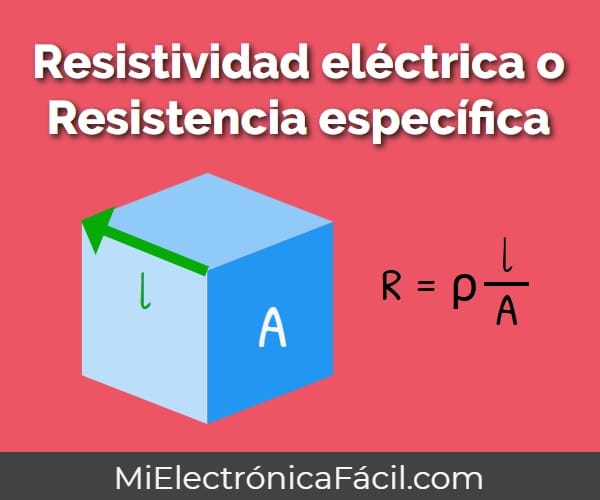
\large\bold{\rho =R \cdot \frac{A}{l}}\large\bold{R = \rho \cdot \frac{l}{A}}Donde
R es la resistencia eléctrica en ohmios (Ω)
l es la longitud del conductor en metros (m)
A es el área de la sección transversal que se mantiene constante en toda la longitud en milímetros cuadrados (m²)
ρ es la resistividad en Ω⋅m
El recíproco de la resistividad se llama conductividad eléctrica.
Explicación de la fórmula
En esta sección presentaremos una breve explicación de la fórmula de la sección anterior en forma de demostración. Además, discutiremos la dependencia de la temperatura de la resistividad con más detalle.
Misma longitud, diferente área transversal
Imagina que tienes dos resistencias delante de ti, que tienen exactamente la misma longitud, pero sus áreas de sección transversal son diferentes. Llamemos a la resistencia del conductor con el área de la sección transversal más pequeña Rm (m de menor) y la de mayor como Rg (g de grande).
Si presentamos la resistencia como una puerta a través de la cual quiere pasar una multitud de personas (representando de la corriente). Adoptando esta analogía, podemos afirmar que:
R_{g} < R_{m}Una puerta más grande (con un área transversal más grande) es más fácil de atravesar para la multitud que una puerta más pequeña (con un área transversal más pequeña). Según la ley de Ohm:
R = \frac{V}{I}Y dado que más corriente fluye a través del conductor con una mayor área de sección transversal, su resistencia Rg es menor.
Misma área transversal, diferente longitud
Consideremos ahora la situación en la que las dos resistencias tienen exactamente la misma área transversal pero diferentes longitudes. Como antes, designamos las resistencias con Rg para el conductor de mayor longitud y Rm para el de menor longitud.
En nuestra analogía con la multitud de personas, cuanto mayor sea la distancia entre la puerta de entrada y la de salida, mayor será la probabilidad de que dos personas choquen. Por lo tanto, una persona puede chocar con otras personas tan a menudo que pierde la orientación y no llega a la puerta de salida.
Esto significa que el flujo de corriente a través del conductor más largo es menor que el del conductor más corto. De nuevo según la ley de Ohm:
R_{g} > R_{m}Podemos expresar estas dos observaciones mediante la siguiente proporcionalidad:
R \thicksim \frac{1}{A}R \thicksim l
Para expresar estas proporciones en forma de una sola ecuación, se introduce la constante de proporcionalidad ρ y se obtiene:
\large\bold{R = \rho \cdot \frac{l}{A}}Esta es la fórmula de la sección anterior, donde ρ es la resistividad.
Dependencia de la temperatura
La resistencia específica tiene una cierta dependencia de la temperatura.
En general, la resistencia de los conductores aumenta cuando la temperatura sube.
Esto se debe al hecho de que los átomos en el conductor oscilan más fuertemente y por lo tanto pueden obstaculizar el movimiento de los electrones a través del conductor con mayor fuerza. Si el cambio de temperatura no es demasiado grande, entonces existe la siguiente relación lineal entre la resistencia eléctrica y el cambio de temperatura.
\rho(T) = \rho(T_0)(1 + \alpha \cdot (T - T_0))
Donde
ρ(T0) es la resistividad a una cierta temperatura de referencia (unos 20 °C)
ρ(T) es la resistividad a una temperatura T
α es el coeficiente de temperatura
Tabla de resistencia específica de distintos materiales
En esta sección presentamos una tabla con las resistencias específicas de algunos materiales determinados.
Resistencia específica a 20 °C
| Material | Resistencia específica en Ω⋅mm²/m |
|---|---|
| Aluminio | 2.65⋅10^-2 |
| Hierro | 1⋅10⁻¹ a 1.5⋅10⁻¹ |
| Germanio | 5⋅10^5 |
| Vidrio | 1⋅10^16 a 1⋅10^21 |
| Constantan | 5⋅10⁻¹ |
| Cobre | 1.721⋅10^-2 |
Dado que la resistencia específica depende de la temperatura, la temperatura para la que se midieron los valores debe especificarse siempre en este tipo de tablas.
Por ejemplo, a 20 ° C, la resistencia específica del cobre es 1.721⋅10^-2 Ω⋅mm²/m y la resistencia específica del aluminio 2.65⋅10^-2 Ω⋅mm²/m.
Ambos son números pequeños, por lo que su conductividad eléctrica es alta. Eso era de esperar, porque el aluminio y el cobre se consideran buenos conductores.
Un aislante como el vidrio, en cambio, tiene una resistencia específica muy alta. Los valores de resistividad para los semiconductores están en algún punto intermedio, aunque no hay límites claros.
Ejercicio resuelto de resistividad específica
1.- Supongamos que tenemos un conductor redondo de cobre de 0.05 m de longitud con un radio de 2 m. ¿Qué resistencia eléctrica tendrá este conductor?
Como es un conductor redondo, podemos calcular el área de la sección transversal de la siguiente manera
A = \pi \cdot r^2 = \pi \cdot (2 \ \mathsf{mm})^2 = 4 \pi \ \mathsf{mm}^2La resistencia eléctrica resulta entonces en:
R = \rho \cdot \frac{l}{A} = 1.721 \cdot 10^{-2} \ \mathsf{\frac{\Omega \cdot mm^2}{m}} \cdot \frac{0,05 \ \mathsf{m}}{4 \pi \ \mathsf{mm}^2} =\bold{ 6.85 \cdot 10^{-5} \ \Omega}Hemos tomado la resistividad del cobre de la tabla de arriba.
Submit your review | |
hctrrdrgz524@gmail.com. Artista de pinceles, gurbias y buriles vivo en Bucaramanga La Ciudad Bonita de Colombia