Leyes de Kirchhoff

• Ley de corrientes de Kirchhoff (primera ley de Kirchhoff)
• Ley de voltajes de Kirchhoff (segunda ley de Kirchhoff)

Estas leyes surgen de la aplicación de la ley de conservación de la energía.

Ley de corrientes de Kirchhoff

Esta ley axiomática se denomina como Ley de corrientes de Kirchhoff (abreviada LCK), la cual simplemente establece que:

La suma algebraica de las corrientes que entran a cualquier nodo es igual a cero.

Esta ley representa un enunciado matemático del hecho de que la carga no se acumula en un nodo. En consecuencia, las corrientes deben sumar cero.

Primera ley de Kirchhoff ejemplos

Se usará la siguiente ilustración para ejemplificar la aplicación de la LCK. En ella se muestran las direcciones del flujo de corriente en un nodo.

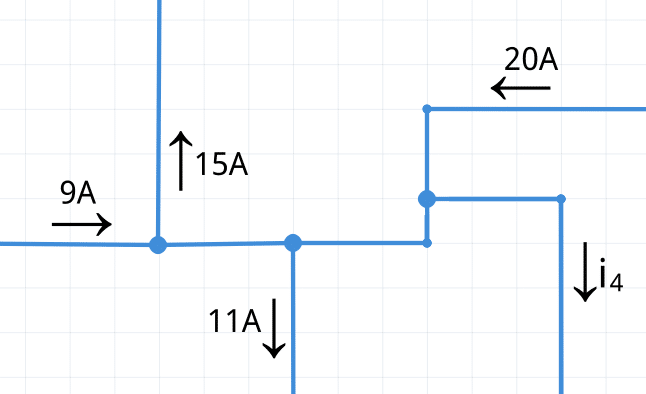
¿Cuál es la corriente i4 en el nodo distribuido?

Esta pregunta pone a prueba tus habilidades con flechas y signos. Las direcciones de las flechas están mezcladas, algunas van hacia adentro, y otras hacia afuera del nodo.

Es recomendable redibujar el nodo con todas las flechas apuntando en la misma dirección. En este caso se dibujan todas hacia afuera.

Si cambias la dirección de una flecha, deberás también cambiar su signo.

Una vez se cambian las direcciones de las corriente y se realizan ajustes a los signos numéricos según sea necesario, se tiene lo siguiente:

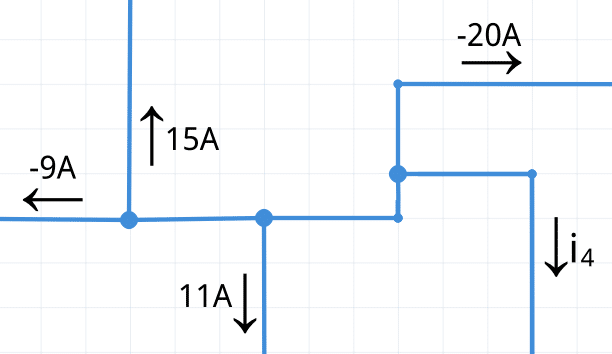
Aplicando la ley de corrientes de Kirchhoff y despejando la corriente i4 se obtiene el valor final de corriente.

LCK Ejercicios

Ejercicio 1: ¿Cuál es la corriente i6 en el nodo distribuido?

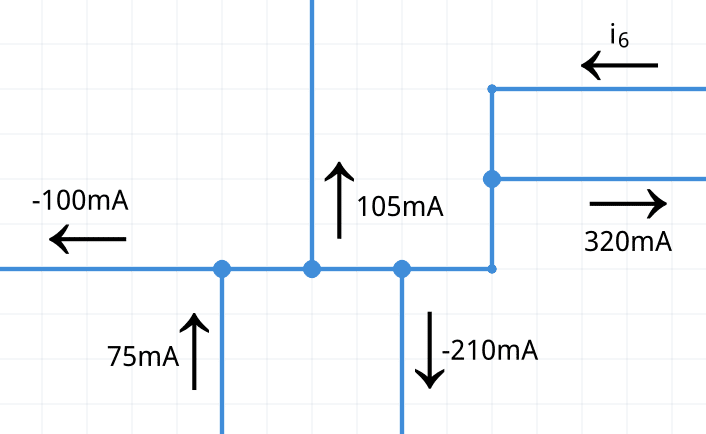
Vuelve a redibujar el circuito con todas las flechas apuntando hacia la misma dirección (hacia afuera o hacia adentro). En este ejemplo se eligen todas las corrientes apuntando hacia afuera; haciendo los ajustes necesarios con las flechas y signos se tiene lo siguiente:

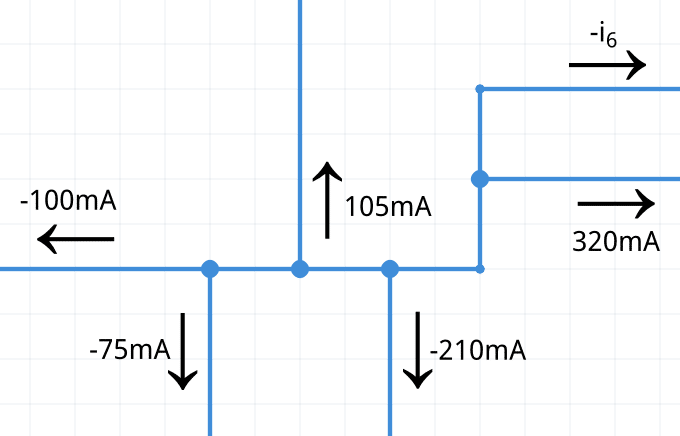
Ahora simplemente se aplica la Ley de corrientes de Kirchhoff y se despeja la incógnita i6.

Ejercicio 2: Encontrar el valor de la suma de las corrientes iA+iB, si iC=37mA e iD=33mA.

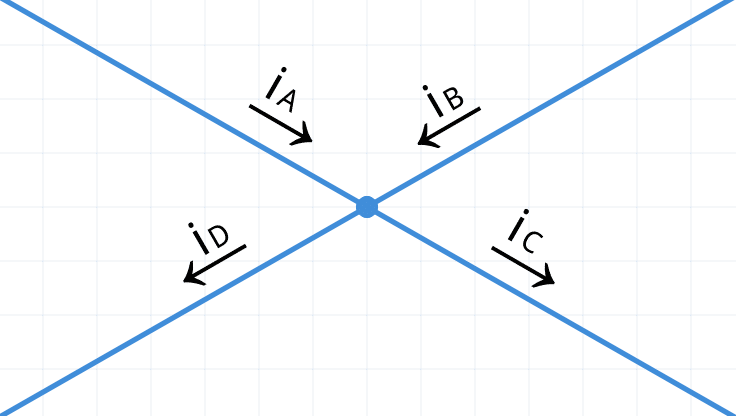
La suma algebraica de las corrientes que entran al nodo debe ser cero:

Entonces, por obviedad, la ley también podría aplicarse de igual manera pero a la suma algebraica de las corrientes que abandonen el nodo:

Ahora, al igualar la suma de las corrientes que tienen flechas de referencia dirigidas hacia el nodo, con la suma de las dirigidas hacia afuera del mismo, y sustituyendo los valores de iC e iD se tiene lo siguiente:

Lo que establece de forma muy sencilla que en este caso la suma de las corrientes que entran es igual a la suma de las corrientes que salen.

Ley de voltajes de Kirchhoff

La ley de voltajes de Kirchhoff (abreviada LVK) es la segunda de las leyes fundamentales que se pueden usar para el análisis de circuitos, la cual simplemente establece que:

La suma algebraica de los voltajes alrededor de cualquier trayectoria cerrada es igual a cero.

En otras palabras, la suma algebraica de TODAS las tensiones alrededor del bucle debe ser igual a cero (ΣV = 0). Ten en cuenta que aquí el término «suma algebraica» significa considerar las polaridades y signos de las fuentes y las caídas de voltaje alrededor el lazo.

Segunda ley de Kirchhoff ejemplos

Con ayuda de la Ley de Tensiones de Kirchhoff, encuentre el voltaje de la resistencia R2.

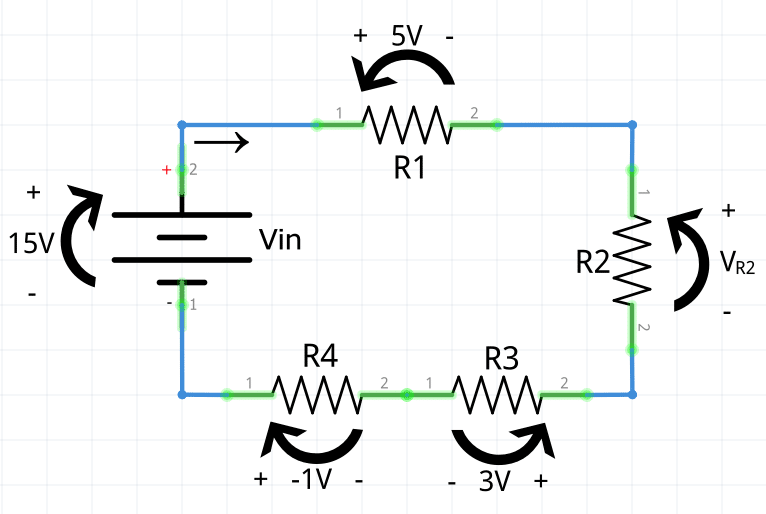
Primero elige un nodo para comenzar el análisis. En este ejemplo se inició con el nodo que conecta R4 con la fuente de voltaje. Ahora sigue el camino en sentido horario alrededor de la trayectoria.

Las flechas de voltaje están mezcladas, no todas apuntan en la misma dirección alrededor de la trayectoria. Entonces, presta mucha atención a la polaridad del voltaje de cada elemento en el bucle. Dependiendo de la dirección de la flecha de voltaje, se define el signo positivo o negativo.

Conseguir los signos correctos para la ecuación es la parte complicada. Esta es la habilidad esencial cuando se aplican las leyes de Kirchhoff. Con ayuda de la LVK se obtiene la siguiente ecuación:

LVK Ejercicios

Ejercicio 1: Calcular el voltaje de cada una de las resistencias del siguiente circuito. Comprobar los resultados con ayuda de la Ley de Voltajes de Kirchhoff.

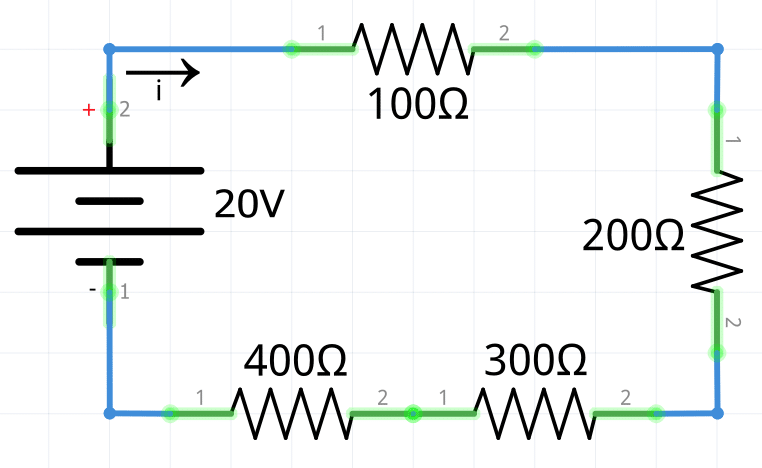
El primer paso para resolver el circuito es calcular la corriente. Luego se calcula el voltaje a través de las resistencias individuales.

Este circuito es un circuito en serie, por lo tanto, solo hay una corriente i que fluye a través de los cinco elementos. Para encontrar la corriente i, las cuatro resistencias en serie se pueden reducir a una sola resistencia equivalente:

Usando la Ley de Ohm, se encuentra la corriente:

Ahora se conoce el valor de la corriente. Con este valor es posible encontrar los voltajes de las cuatro resistencias. Regresando al esquema original y agregando etiquetas de voltaje a los cinco elementos se tiene:

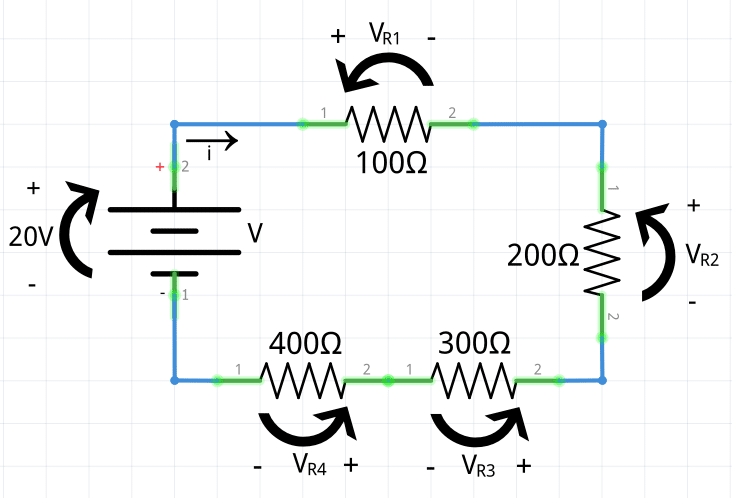
Finalmente, se aplica la Ley de Ohm cuatro veces para encontrar el voltaje en cada resistencia:

Para comprobar que los resultados son correctos utilice la LVK.

Resumen